题目内容
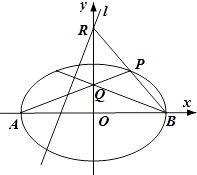
【题目】已知双曲线![]() (a>b>0)的左、右焦点分别是F1,F2,过F2的直线交双曲线的右支于P,Q两点,若|PF1|=|F1F2|,且3|PF2|=2|QF2|,则该双曲线的离心率为 ( )
(a>b>0)的左、右焦点分别是F1,F2,过F2的直线交双曲线的右支于P,Q两点,若|PF1|=|F1F2|,且3|PF2|=2|QF2|,则该双曲线的离心率为 ( )
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
【答案】D
【解析】
连接![]() ,利用题设条件和双曲线的定义分别求得求得
,利用题设条件和双曲线的定义分别求得求得![]() ,再在
,再在![]() 和
和![]() 中,利用余弦定理求得
中,利用余弦定理求得![]() 和
和![]() ,又由
,又由![]() ,即可化简得到答案.
,即可化简得到答案.
连接F1Q,设F1(-c,0),F2(c,0),则|PF1|=|F1F2|=2c.
由双曲线的定义可得|PF2|=|PF1|-2a=2c-2a,
∴由3|PF2|=2|QF2|,可得|QF2|=3c-3a,
∴由双曲线的定义可得|QF1|=|QF2|+2a=3c-a.
在△PF1F2和△QF1F2中,cos∠F1F2P=![]() =
=![]() =
=![]() ,
,
cos∠F1F2Q=![]() =
=![]() =
=![]() .
.
由∠F1F2Q+∠F1F2P=π,可得cos∠F1F2Q+cos∠F1F2P=0,
即有![]() +
+![]() =0,化简得5c=7a,所以e==.
=0,化简得5c=7a,所以e==.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目