题目内容
4.一个正方体的棱长为m,表面积为n,一个球的半径为p,表面积为q,若$\frac{m}{p}$=2,则$\frac{n}{q}$=( )| A. | $\frac{8}{π}$ | B. | $\frac{6}{π}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{8}$ |
分析 利用正方体、球的表面积公式,结合条件,即可得出结论.
解答 解:因为n=6m2,q=4πp2,
所以$\frac{n}{q}$=$\frac{6{m}^{2}}{4π{p}^{2}}$=$\frac{6}{4π}•(\frac{m}{p})^{2}$=$\frac{6}{π}$.
故选:B.
点评 本题考查正方体、球的表面积公式,考查学生的计算能力,比较基础.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
14.已知f(x)=$\left\{\begin{array}{l}{x+2(x≤-1)}\\{{x}^{2}(x>-1)}\end{array}\right.$,若f(x)=3,则x的值是( )
| A. | 1 | B. | 1或±$\sqrt{3}$ | C. | ±$\sqrt{3}$ | D. | $\sqrt{3}$ |
15.已知sinx+cosx=$\sqrt{1+sin2x}$,则x的取值范围是( )
| A. | [-$\frac{π}{4}$+kπ,$\frac{π}{4}$+kπ](k∈Z) | B. | [$\frac{π}{4}$+kπ,$\frac{3π}{4}$+kπ](k∈Z) | ||
| C. | [-$\frac{π}{4}$+2kπ,$\frac{3π}{4}$+2kπ](k∈Z) | D. | [$\frac{π}{4}$+2kπ,$\frac{5π}{4}$+2kπ](k∈Z) |
9.已知直线l经过点A(4,1),B(6,3),则直线l的倾斜角是( )
| A. | 0° | B. | 30° | C. | 45° | D. | 60° |
16.运行如图的程序框图,则输出s的结果是( )
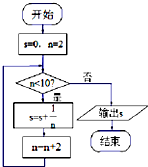

| A. | $\frac{25}{24}$ | B. | $\frac{1}{6}$ | C. | $\frac{3}{4}$ | D. | $\frac{11}{12}$ |