题目内容
16.运行如图的程序框图,则输出s的结果是( )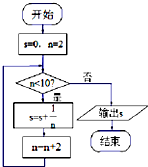
| A. | $\frac{25}{24}$ | B. | $\frac{1}{6}$ | C. | $\frac{3}{4}$ | D. | $\frac{11}{12}$ |
分析 模拟程序框图的运行过程,即可得出该程序运行后输出的s值是什么.
解答 解:模拟程序框图的运行过程,得:
s=0,n=2,n<10?,是,s=0+$\frac{1}{2}$=$\frac{1}{2}$;
n=4,n<10?,是,s=$\frac{1}{2}$+$\frac{1}{4}$=$\frac{3}{4}$;
n=6,n<10?,是,s=$\frac{3}{4}$+$\frac{1}{6}$=$\frac{11}{12}$;
n=8,n<10?,是,s=$\frac{11}{12}$+$\frac{1}{8}$=$\frac{25}{24}$;
n=10,n<10?,否,输出s=$\frac{25}{24}$.
故选:A.
点评 本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,是基础题目.

练习册系列答案
相关题目
7.某中学为了解学校办公楼每天的用电量x(度)与当天最高气温x(℃)之间的关系,随机统计了近期某4天的有关数据如下表示:
据回归分析,上述4线样本数据具有线性相关关系,计算得回归直线的斜率b=-3.2,由回归方程可以预报最高气温为6℃时当天的用电量约为( )
| 最高气温x(℃) | 10 | 4 | -2 | -8 |
| 用电量y(度) | 20 | 44 | 56 | 80 |
| A. | 32度 | B. | 34度 | C. | 36度 | D. | 38度 |
4.一个正方体的棱长为m,表面积为n,一个球的半径为p,表面积为q,若$\frac{m}{p}$=2,则$\frac{n}{q}$=( )
| A. | $\frac{8}{π}$ | B. | $\frac{6}{π}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{8}$ |
8.直线x=0的斜率为( )
| A. | 0 | B. | $\frac{π}{2}$ | C. | 1 | D. | 不存在 |
6.已知全集U=R,A={x|2<3x≤9},B={y|$\frac{1}{2}$<y≤2},则有( )
| A. | A?B | B. | A∩B=B | C. | A∩(∁RB)≠∅ | D. | A∪(∁RB)=R |