题目内容
【题目】已知函数![]() 在其定义域内有两个不同的零点.
在其定义域内有两个不同的零点.
(1)求![]() 的取值范围;
的取值范围;
(2)记两个零点为![]() ,且
,且![]() ,已知
,已知![]() ,若不等式
,若不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]()
(2)![]()
【解析】
(1)根据零点与方程的关系,分离参数后构造函数![]() ,并求得
,并求得![]() ,结合导函数的符号判断
,结合导函数的符号判断![]() 的单调性,从而求得最大值;由
的单调性,从而求得最大值;由![]() 时
时![]() 的极限,即可确定函数
的极限,即可确定函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同交点时
上有两个不同交点时![]() 的取值范围;
的取值范围;
(2)根据零点定义,将![]() 代入可得
代入可得![]() ,
,![]() .再结合不等式代入化简并分离参数
.再结合不等式代入化简并分离参数![]() ;由
;由![]() ,
,![]() ,作差也可分离参数
,作差也可分离参数![]() ,将两个式子合并化简,令
,将两个式子合并化简,令![]() ,再构造函数
,再构造函数![]() ,再求得
,再求得![]() ,对
,对![]() 分类讨论,由
分类讨论,由![]() 的单调性与极值,即可确定
的单调性与极值,即可确定![]() 的取值范围.
的取值范围.
(1)依题意,函数![]() 在定义域
在定义域![]() 上有两个不同的零点,即方程
上有两个不同的零点,即方程![]() 在
在![]() )上有两个不同的解,也即
)上有两个不同的解,也即![]() 在
在![]() 上有两个不同的解.
上有两个不同的解.
令![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调逆增,
上单调逆增,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() .
.
又![]() ,
,![]() 时,
时,![]()
当![]() 时,
时,![]() ,且
,且![]() ,
,
若函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同的交点,
上有两个不同的交点,
则![]() .
.
(2)因为![]() 为方程
为方程![]() 的两根,
的两根,
所以![]() ,
,![]() .
.
不等式![]() ,变形可得
,变形可得![]() ,
,
代入可得![]() .
.
因为![]() ,
,![]() ,所以原不等式等价于
,所以原不等式等价于![]() .
.
又由![]() ,
,![]() ,作差得
,作差得![]() ,所以
,所以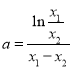 .
.
所以原不等式等价于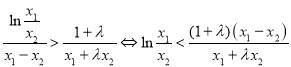 恒成立.
恒成立.
令![]() ,则
,则![]() ,不等式等价于
,不等式等价于![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,则
,则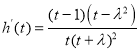 .
.
①当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递,因此
上单调递,因此![]() ,满足条件;
,满足条件;
②当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,又
上单调递减,又![]() ,所以
,所以![]() 在
在![]() 上不能恒小于零.
上不能恒小于零.
综上,![]() .
.

【题目】2019年,中华人民共和国成立70周年,为了庆祝建国70周年,某中学在全校进行了一次爱国主义知识竞赛,共1000名学生参加,答对题数(共60题)分布如下表所示:
组别 |
|
|
|
|
|
|
频数 | 10 | 185 | 265 | 400 | 115 | 25 |
答对题数![]() 近似服从正态分布
近似服从正态分布![]() ,
,![]() 为这1000人答对题数的平均值(同一组数据用该组区间的中点值作为代表).
为这1000人答对题数的平均值(同一组数据用该组区间的中点值作为代表).
(1)估计答对题数在![]() 内的人数(精确到整数位).
内的人数(精确到整数位).
(2)学校为此次参加竞赛的学生制定如下奖励方案:每名同学可以获得2次抽奖机会,每次抽奖所得奖品的价值与对应的概率如下表所示.
获得奖品的价值(单位:元) | 0 | 10 | 20 |
概率 |
|
|
|
用![]() (单位:元)表示学生甲参与抽奖所得奖品的价值,求
(单位:元)表示学生甲参与抽奖所得奖品的价值,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
【题目】某便利店计划每天购进某品牌鲜奶若干件,便利店每销售一瓶鲜奶可获利![]() 元;若供大于求,剩余鲜奶全部退回,但每瓶鲜奶亏损
元;若供大于求,剩余鲜奶全部退回,但每瓶鲜奶亏损![]() 元;若供不应求,则便利店可从外调剂,此时每瓶调剂品可获利
元;若供不应求,则便利店可从外调剂,此时每瓶调剂品可获利![]() 元.
元.
(1)若便利店一天购进鲜奶![]() 瓶,求当天的利润
瓶,求当天的利润![]() (单位:元)关于当天鲜奶需求量
(单位:元)关于当天鲜奶需求量![]() (单位:瓶,
(单位:瓶,![]() )的函数解析式;
)的函数解析式;
(2)便利店记录了![]() 天该鲜奶的日需求量
天该鲜奶的日需求量![]() (单位:瓶,
(单位:瓶,![]() )整理得下表:
)整理得下表:
日需求量 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
若便利店一天购进![]() 瓶该鲜奶,以
瓶该鲜奶,以![]() 天记录的各需求量的频率作为各需求量发生的概率,求当天利润在区间
天记录的各需求量的频率作为各需求量发生的概率,求当天利润在区间![]() 内的概率.
内的概率.