题目内容

1．（x-3）n的展开式中只有第3项的二项式系数最大，则n为（　　）
A．3B．4C．5D．6

分析 由题意结合二项式系数的性质，可知二项展开式中仅有5项，则n可求．

解答 解：∵（x-3）n的展开式中只有第3项的二项式系数最大，
∴（x-3）n的展开式中只有5项，则n=4．
故选：B．

点评 本题考查二项式系数的性质，当n为偶数时，只有中间一项的二项式系数最大，是基础题．

练习册系列答案
相关题目
11．若向量$\overrightarrow a，\vec b$满足$|{\vec a}|=1，|{\vec b}|=2$且$|{2\vec a+\vec b}|=2\sqrt{3}$，则向量$\overrightarrow a，\vec b$的夹角为（　　）
A．$\frac{2π}{3}$B．$\frac{π}{2}$C．$\frac{π}{3}$D．$\frac{π}{6}$
12．设二次函数f（x）=（k-4）x2+kx，（k∈R），对任意实数x，有f（x）≤6x+2恒成立；数列{an}满足an+1=f（an）．
（1）求函数f（x）的解析式和值域；
（2）已知a1=$\frac{1}{3}$，是否存在非零整数λ，使得对任意n∈N*，都有${log_3}（{\frac{1}{{\frac{1}{2}-{a_1}}}}）+{log_3}（{\frac{1}{{\frac{1}{2}-{a_2}}}}）+…+{log_3}（{\frac{1}{{\frac{1}{2}-{a_n}}}}）＞{（{-1}）^{n-1}}2λ+n{log_3}$2-1-1+（-1）n-12λ+nlog32恒成立，若存在，求之；若不存在，说明理由．
9．已知数列{an}中，a1=5，Sn+1=2Sn+n+5（n∈N+）
（1）证明：{an+1} 数列是等比数列．
（2）求数列 {an}的前n项和Sn．
16．为了调查甲、乙两个交通站的车流量，随机选取了14天，统计每天上午8：00-12：00间各自的车流量（单位：百辆），得如下所示的统计图，
（1）甲、乙两个交通站的车流量的极差分别是多少？
（2）甲交通站的车流量在[10，40]间的频率是多少？
（3）甲、乙两个交通站哪个站更繁忙？并说明理由．
6．已知F1、F2为椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{169}$=1的两个焦点，过F1的直线交椭圆于A、B两点．若|F2A|+|F2B|=30，则|AB|=（　　）
A．16B．18C．22D．20
13．U=x2+y2+1与V=2（x+y-1）的大小关系是U＞V．
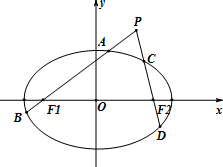2．如图，已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左右焦点分别为F1，F2，离心率为$\frac{{\sqrt{2}}}{2}$，它的四个顶点连成的菱形的面积为8$\sqrt{2}$．过动点P（不在x轴上）的直线PF1，PF2与椭圆的交点分别为A，B和C，D．
（1）求此椭圆的标准方程；
（2）是否存在点P，使|AB|=2|CD|，若存在求出点P的坐标；若不存在，请说明理由．
3．已知点P（x，y）的坐标满足|x|+|y|≤1，那么2x+y的最小值是（　　）
A．-3B．-2C．-1D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网