Question

【题目】已知函数f（x）=3x2﹣2ax﹣b，其中a，b是实数．
（1）若不等式f（x）≤0的解集是[0，6]，求ab的值；
（2）若b=3a，对任意x∈R，都有f（x）≥0，且存在实数x，使得f（x）≤2﹣ a，求实数a的取值范围；
（3）若方程有一个根是1，且a，b＞0，求 的最小值，及此时a，b的值．

Answer 1

【答案】
（1）解：依题意，0+6= ，0×6= ，解得a=9，b=0，∴ab=1
（2）解：若b=3a，则f（x）=3x2﹣2ax﹣3a．

依题意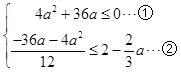， ，由①得，﹣9≤a≤0，

由②得，a≥0或a≤﹣6，

所以，﹣9≤a≤﹣6或a=0为所求

（3）解：∵方程有一个根是1，且a、b＞0，∴3﹣2a﹣b=0，即2a+b=3，

∵2a+b=3可得（2a+1）（b+2）=6，

设u=2a+1，v=b+2，可得u，v＞0，u+v=6，

= = ≥ ，

当且仅当u=v=3，即a=b=1时取等号

【解析】（1）利用不等式的解集，转化为方程的根，求解即可．（2）利用二次函数的性质，列出不等式组求解即可．（3）利用基本不等式转化求解函数的最值的即可．
【考点精析】掌握函数的最值及其几何意义是解答本题的根本，需要知道利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值．