题目内容
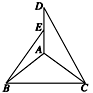
如图所示,等腰直角三角形ABC中,∠A=90°,BC=![]() ,DA⊥AC,DA⊥AB,若DA=1,且E为DA的中点.求异面直线BE与CD所成角的余弦值.
,DA⊥AC,DA⊥AB,若DA=1,且E为DA的中点.求异面直线BE与CD所成角的余弦值.
异面直线BE与CD所成角的余弦值为![]()
解析:
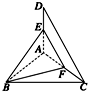
取AC的中点F,连接EF,BF,在△ACD中,E、F分别是AD、AC的中点,
∴EF∥CD,
∴∠BEF即为异面直线BE与CD所成的角或其补角.
在Rt△EAB中,AB=AC=1,
 AE=
AE=![]() AD=
AD=![]() ,∴BE=
,∴BE=![]() ,
,
在Rt△EAF中,
AF=![]() AC=
AC=![]() ,AE=
,AE=![]() ,∴EF=
,∴EF=![]() ,
,
在Rt△BAF中,AB=1,AF=![]() ,∴BF=
,∴BF=![]() ,
,
在等腰三角形EBF中,
cos∠FEB=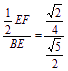 =
=![]() ,
,
∴异面直线BE与CD所成角的余弦值为![]() .
.

练习册系列答案
相关题目
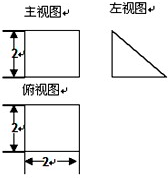 三棱柱三视图(主视图和俯视图是正方形,左视图是等腰直角三角形)如图所示,则这个三棱柱的全面积等于
三棱柱三视图(主视图和俯视图是正方形,左视图是等腰直角三角形)如图所示,则这个三棱柱的全面积等于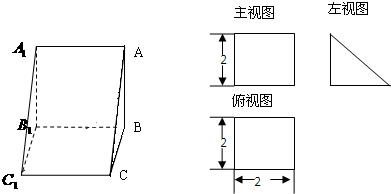 (2012•韶关一模)三棱柱的直观图和三视图(主视图和俯视图是正方形,左视图是等腰直角三角形)如图所示,则这个三棱柱的全面积等于( )
(2012•韶关一模)三棱柱的直观图和三视图(主视图和俯视图是正方形,左视图是等腰直角三角形)如图所示,则这个三棱柱的全面积等于( ) (三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) 如图所示,在直三棱柱ABC-A1B1C1中,底面是∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF=
如图所示,在直三棱柱ABC-A1B1C1中,底面是∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF=