题目内容
如图所示，在直三棱柱ABC-A1B1C1中，底面是∠ABC为直角的等腰直角三角形，AC=2a，BB1=3a，D是A1C1的中点，点F在线段AA1上，当AF=a或2a
a或2a
时，CF⊥平面B1DF．分析：利用已知条件判断B1D⊥平面AC1，然后说明CF⊥DF．设AF=x（0＜x＜3a），通过CF2=x2+4a2，DF2=a2+（3a-x）2，又CD2=a2+9a2=10a2，求出x即可．
解答：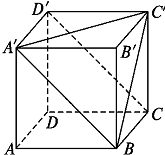
解：由已知得B1D⊥平面AC1，
又CF?平面AC1，∴B1D⊥CF，
故若CF⊥平面B1DF，则必有CF⊥DF．
设AF=x（0＜x＜3a），则CF2=x2+4a2，
DF2=a2+（3a-x）2，又CD2=a2+9a2=10a2，
∴10a2=x2+4a2+a2+（3a-x）2，
解得x=a或2a．
故答案为：a或2a．
解：由已知得B1D⊥平面AC1，又CF?平面AC1，∴B1D⊥CF，
故若CF⊥平面B1DF，则必有CF⊥DF．
设AF=x（0＜x＜3a），则CF2=x2+4a2，
DF2=a2+（3a-x）2，又CD2=a2+9a2=10a2，
∴10a2=x2+4a2+a2+（3a-x）2，
解得x=a或2a．
故答案为：a或2a．
点评：本题考查直线与平面的位置关系，考查空间想象能力以及计算能力．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
如图所示，在直三棱柱ABC-A1B1C1中，AC⊥BC，AA1=AC=BC=2，D、E、F分别是AB、AA1、CC1的中点，P是CD上的点．
如图所示，在直三棱柱ABC-A′B′C′中，∠BAC=90°，AB=BB′=1，直线B′C与平面ABC成30°角．
如图所示，在直三棱柱ABC-A1B1C1中，AB=BB1，AC1⊥平面A1BD，D为AC的中点．
如图所示，在直三棱柱ABC-A1B1C1中，AB=BB1=BC，AC1⊥平面A1BD，D为AC的中点．