题目内容
【题目】已知a,b为常数,a0,函数![]() .
.
(1)若a=2,b=1,求![]() 在(0,+∞)内的极值;
在(0,+∞)内的极值;
(2)①若a>0,b>0,求证:![]() 在区间[1,2]上是增函数;
在区间[1,2]上是增函数;
②若![]() ,
,![]() ,且
,且![]() 在区间[1,2]上是增函数,求由所有点
在区间[1,2]上是增函数,求由所有点![]() 形成的平面区域的面积.
形成的平面区域的面积.
【答案】(1)![]() ,(2)①详见解析,②
,(2)①详见解析,②![]()
【解析】
试题分析:(1)求具体函数极值问题分三步,一是求导,二是求根,三是列表,关键在于正确求出导数,即![]() ;求根时需结合定义区间进行取舍,如根据定义区间
;求根时需结合定义区间进行取舍,如根据定义区间![]() 舍去负根;列表时需注意导数在对应区间的符号变化规律,这样才可得出正确结论,因为导数为零的点不一定为极值点,极值点附近导数值必须要变号,(2)①利用导数证明函数单调性,首先要正确转化,如本题只需证到在区间[1,2]上
舍去负根;列表时需注意导数在对应区间的符号变化规律,这样才可得出正确结论,因为导数为零的点不一定为极值点,极值点附近导数值必须要变号,(2)①利用导数证明函数单调性,首先要正确转化,如本题只需证到在区间[1,2]上![]() 成立即可,由
成立即可,由![]() 得只需证到在区间[1,2]上
得只需证到在区间[1,2]上![]() ,因为对称轴
,因为对称轴![]()
![]() 在区间[1,2]上单调增,因此只需证
在区间[1,2]上单调增,因此只需证![]() ,而这显然成立,②中条件“
,而这显然成立,②中条件“![]() 在区间[1,2]上是增函数”与①不同,它是要求
在区间[1,2]上是增函数”与①不同,它是要求![]() 在区间[1,2]上恒成立,结合二次函数图像可得关于
在区间[1,2]上恒成立,结合二次函数图像可得关于![]() 不等关系,再考虑
不等关系,再考虑![]() ,
,![]() ,可得可行域.
,可得可行域.
试题解析:(1)解:![]() 2分
2分
当![]() 时,
时,![]() ,
,
令![]() 得
得![]() 或
或![]() (舍去) 4分
(舍去) 4分
![]() 当
当![]() 时,
时,![]()
![]() 是减函数,
是减函数,
当![]() 时,
时,![]()
![]() 是增函数
是增函数
所以当![]() 时,
时,![]() 取得极小值为
取得极小值为![]() 6分
6分
(2)令![]()
①证明:![]() 二次函数
二次函数![]() 的图象开口向上,
的图象开口向上,
对称轴![]() 且
且![]() 8分
8分
![]() 对一切
对一切![]() 恒成立.
恒成立.
又![]()
![]() 对一切
对一切![]() 恒成立.
恒成立.
![]() 函数图象是不间断的,
函数图象是不间断的,
![]() 在区间
在区间![]() 上是增函数. 10分
上是增函数. 10分
②解:![]()
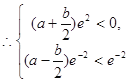 即
即![]()
![]() 在区间
在区间![]() 上是增函数
上是增函数
![]() 对
对![]() 恒成立.
恒成立.
则![]() 对
对![]() 恒成立.
恒成立.
![]() 12分
12分
在(*)(**)的条件下,![]() 且
且![]()
且![]() 恒成立.
恒成立.
综上,点![]() 满足的线性约束条件是
满足的线性约束条件是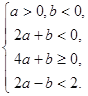 14分
14分
由所有点![]() 形成的平面区域为
形成的平面区域为![]() (如图所示),
(如图所示),
其中![]()
则![]()
即![]() 的面积为
的面积为![]() . 16分
. 16分

 名校课堂系列答案
名校课堂系列答案【题目】近年来,网络电商已经悄然进入了广大市民的日常生活,并慢慢改变了人们的消费方式为了更好地服务民众,某电商在其官方APP中设置了用户评价反馈系统,以了解用户对商品状况和优惠活动的评价现从评价系统中随机抽出200条较为详细的评价信息进行统计,商品状况和优惠活动评价的2×2列联表如下:
对优惠活动好评 | 对优惠活动不满意 | 合计 | |
对商品状况好评 | 100 | 20 | 120 |
对商品状况不满意 | 50 | 30 | 80 |
合计 | 150 | 50 | 200 |
(I)能否在犯错误的概率不超过0.001的前提下认为优惠活动好评与商品状况好评之间有关系?
(Ⅱ)为了回馈用户,公司通过APP向用户随机派送每张面额为0元,1元,2元的三种优惠券用户每次使用APP购物后,都可获得一张优惠券,且购物一次获得1元优惠券,2元优惠券的概率分别是![]() ,
,![]() ,各次获取优惠券的结果相互独立若某用户一天使用了APP购物两次,记该用户当天获得的优惠券面额之和为X,求随机变量X的分布列和数学期望.
,各次获取优惠券的结果相互独立若某用户一天使用了APP购物两次,记该用户当天获得的优惠券面额之和为X,求随机变量X的分布列和数学期望.
参考数据
P(K2≥k) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:K2![]() ,其中n=a+b+c+d
,其中n=a+b+c+d



