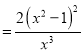Question

【题目】某公园欲将一块空地规划成如图所示的区域，其中在边长为20米的正方形内种植经红色郁金香，在正方形的剩余部分（即四个直角三角形内）种植黄色郁金香．现要在以为边长的矩形内种植绿色草坪，要求绿色草坪的面积等于黄色郁金香的面积．设，米．

（1）求与之间的函数关系式；

（2）求的最大值．

Answer 1

【答案】（1），其中（2）米

【解析】

（1）利用已知条件将黄色郁金香和绿色草坪的面积表示出来，然后根据面积相等，得到与之间的函数关系式，注意定义域；

（2）根据，用换元法并构造新函数完成最大值的求解.

解：（1）在中，，则，

同理，在中，，则，

所以．

因为在矩形内种植与黄花面积相等的草坪，

设矩形的面积为，则，

所以，

所以，其中．

（2）令，则．

因为，所以，

所以，因为在上单调递增，

所以，

答：的最大值为米．