题目内容
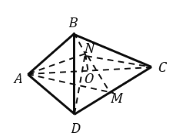
【题目】如图,在四棱锥![]() 中,
中,![]() 是以
是以![]() 为斜边的直角三角形,
为斜边的直角三角形,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)若线段![]() 上有一个点
上有一个点![]() ,使得
,使得![]() 平面
平面![]() ,请确定点
,请确定点![]() 的位置,并说明理由;
的位置,并说明理由;
(2)若平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)当P为AD的中点时,![]() 平面PBE(2)
平面PBE(2)![]()
【解析】
要证线面平行,需证明线线平行,所以取![]() 中点
中点![]() ,连接
,连接![]() ,即证明
,即证明![]() ;
;
(2)过B作![]() 于H,连结HE,证明
于H,连结HE,证明![]() 两两垂直,以点
两两垂直,以点![]() 为原点,建立空间直角坐标系,求平面
为原点,建立空间直角坐标系,求平面![]() 的法向量
的法向量![]() ,利用公式
,利用公式![]() 求解.
求解.
解:(1)当P为AD的中点时,![]() ,
,
又因为![]() 平面PBE,
平面PBE,![]() 平面PBE,所以
平面PBE,所以![]() 平面PBE.
平面PBE.
(2)过B作![]() 于H,连结HE,在等腰梯形ABCD中易知
于H,连结HE,在等腰梯形ABCD中易知![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,可得
,可得![]() .
.
又因为![]() ,平面
,平面![]() 平面ADE,
平面ADE,
且平面![]() 平面
平面![]() ,
,
所以![]() 平面ADE,所以
平面ADE,所以![]() .
.
如图,以H为原点,HE,HD,HB所在直线分别为x轴,y轴,z轴建立空间直角坐标系.
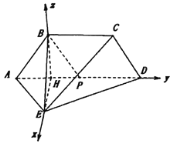
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() .
.![]() .设平面ABE的一个法向量
.设平面ABE的一个法向量![]() ,
,
则![]() ,即
,即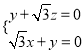 ,取
,取![]() ,得
,得![]() .
.
设直线CD与平面ABE所成角为![]() ,所以
,所以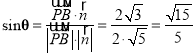 .
.

【题目】近年来,国资委.党委高度重视扶贫开发工作,坚决贯彻落实中央扶贫工作重大决策部署,在各个贫困县全力推进定点扶贫各项工作,取得了积极成效,某贫困县为了响应国家精准扶贫的号召,特地承包了一块土地,已知土地的使用面积以及相应的管理时间的关系如下表所示:
土地使用面积 | 1 | 2 | 3 | 4 | 5 |
管理时间 | 8 | 10 | 13 | 25 | 24 |
并调查了某村300名村民参与管理的意愿,得到的部分数据如下表所示:
愿意参与管理 | 不愿意参与管理 | |
男性村民 | 150 | 50 |
女性村民 | 50 |
(1)求出相关系数![]() 的大小,并判断管理时间
的大小,并判断管理时间![]() 与土地使用面积
与土地使用面积![]() 是否线性相关?
是否线性相关?
(2)是否有99.9%的把握认为村民的性别与参与管理的意愿具有相关性?
(3)若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况,则从该贫困县中任取3人,记取到不愿意参与管理的男性村民的人数为![]() ,求
,求![]() 的分布列及数学期望。
的分布列及数学期望。
参考公式:

![]()
其中![]() 。临界值表:
。临界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参考数据:![]()
【题目】作为加班拍档、创业伴侣、春运神器,曾几何时,方便面是我们生活中重要的“朋友”,然而这种景象却在近![]() 年出现了戏剧性的逆转.统计显示.2011年之前,方便面销量在中国连续
年出现了戏剧性的逆转.统计显示.2011年之前,方便面销量在中国连续![]() 年保持两位数增长,2013年的年销量更是创下
年保持两位数增长,2013年的年销量更是创下![]() 亿包的辉煌战绩;但2013年以来,方便面销量却连续3年下跌,只剩
亿包的辉煌战绩;但2013年以来,方便面销量却连续3年下跌,只剩![]() 亿包,具体如下表.相较于方便面,网络订餐成为大家更加青睐的消费选择.近年来,网络订餐市场规模的“井喷式”增长,也充分反映了人们消费方式的变化.
亿包,具体如下表.相较于方便面,网络订餐成为大家更加青睐的消费选择.近年来,网络订餐市场规模的“井喷式”增长,也充分反映了人们消费方式的变化.
全国方便面销量情况(单位“亿包/桶)(数据来源:世界方便面协会)
年份 |
|
|
|
|
时间代号 |
|
|
|
|
年销量 |
|
|
|
|
(1)根据上表,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .用所求回归方程预测2017 年(
.用所求回归方程预测2017 年(![]() )方便面在中国的年销量;
)方便面在中国的年销量;
(2)方便面销量遭遇滑铁卢受到哪些因素影响? 中国的消费业态发生了怎样的转变? 某媒体记者随机对身边的![]() 位朋友做了一次调查,其中
位朋友做了一次调查,其中![]() 位受访者表示超过
位受访者表示超过![]() 年未吃过方便面,
年未吃过方便面,![]() 位受访者认为方便面是健康食品;而
位受访者认为方便面是健康食品;而![]() 位受访者有过网络订餐的经历,现从这
位受访者有过网络订餐的经历,现从这![]() 人中抽取
人中抽取![]() 人进行深度访谈,记
人进行深度访谈,记![]() 表示随机抽取的
表示随机抽取的![]() 人认为方便面是健康食品的人数,求随机变量
人认为方便面是健康食品的人数,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
参考公式:回归方程:![]() ,其中
,其中 ,
,![]() .
.
参考数据:![]() .
.