题目内容
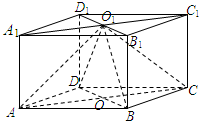 如图,直四棱柱ABCD-A1B1C1D1的高为3,底面是边长为4的菱形,且∠DAB=60°,AC∩BD=O,A1C1∩B1D1=O1,
如图,直四棱柱ABCD-A1B1C1D1的高为3,底面是边长为4的菱形,且∠DAB=60°,AC∩BD=O,A1C1∩B1D1=O1,(1)求证:平面O1AC⊥平面O1BD;
(2)求二面角O1-BC-D的大小.
分析:(1)证明平面O1AC⊥平面O1BD. 只需要证明面O1BD中的一条直线垂直于平面O1AC,即证BD⊥面O1AC;
(2)用立体几何法,作出它的平面角,过O作OH⊥BC于H,连接O1H,则∠O1HO为二面角O1-BC-D的平面角,再求之
(2)用立体几何法,作出它的平面角,过O作OH⊥BC于H,连接O1H,则∠O1HO为二面角O1-BC-D的平面角,再求之
解答:(1)证明:∵ABCD-A1B1C1D1是直四棱柱,
∴AA1⊥面AC,
又BD?面AC,所以AA1⊥BD. (2分)
又∵ABCD是菱形,∴AC⊥BD
∵AA1∩AC=A
所以BD⊥面AA1C. (4分)
即BD⊥面O1AC,又BD?面O1BD,
所以平面O1AC⊥平面O1BD. (6分)
(2)解:过O作OH⊥BC于H,连接O1H,则∠O1HO为二面角O1-BC-D的平面角. (8分)
在Rt△BHO中,OB=2,∠OBH=60°,∴OH=
. (10分)
又O1O∥A1A,∴O1O⊥OH.
∴tan∠O1OH=
=
⇒∠O1HO=
.
故二面角O1-BC-D的大小为
. (12分)
(注:向量解法,酌情给分)
∴AA1⊥面AC,
又BD?面AC,所以AA1⊥BD. (2分)
又∵ABCD是菱形,∴AC⊥BD
∵AA1∩AC=A
所以BD⊥面AA1C. (4分)
即BD⊥面O1AC,又BD?面O1BD,
所以平面O1AC⊥平面O1BD. (6分)
(2)解:过O作OH⊥BC于H,连接O1H,则∠O1HO为二面角O1-BC-D的平面角. (8分)
在Rt△BHO中,OB=2,∠OBH=60°,∴OH=
| 3 |
又O1O∥A1A,∴O1O⊥OH.
∴tan∠O1OH=
| O1O |
| OH |
| 3 |
| π |
| 3 |
故二面角O1-BC-D的大小为
| π |
| 3 |
(注:向量解法,酌情给分)
点评:本题以直四棱柱为载体,考查面面垂直,考查面面角,解题的关键是利用面面垂直的判定,正确作出面面角.

练习册系列答案
相关题目
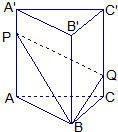 如图:直三棱柱ABC-A′B′C′的体积为V,点P、Q分别在侧棱AA′和CC′上,AP=C′Q,则四棱锥B-APQC的体积为
如图:直三棱柱ABC-A′B′C′的体积为V,点P、Q分别在侧棱AA′和CC′上,AP=C′Q,则四棱锥B-APQC的体积为 如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2.
如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2. 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8. (2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点.
(2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点. 如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.