题目内容
 如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2.
如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2.(1)求证:AB1∥平面BC1D;
(2)若四棱锥B-DAA1C1的体积为2,求二面角C-BC1-D的正切值.
分析:(1)证明AB1∥平面BC1D,可在平面BC1D内找到一条与AB1平行的直线,而D为AC中点,可联想连结B1C,得到其中点O,由三角形的中位线定理可得要找的平行线,则问题得证;
(2)由给出的四棱锥的体积,求出BC的长度,过D作BC的垂线DF,再由F作FG垂直于BC1,连结DG找出要求的二面角的平面角,然后通过解直角三角形得到二面角C-BC1-D的正切值.
(2)由给出的四棱锥的体积,求出BC的长度,过D作BC的垂线DF,再由F作FG垂直于BC1,连结DG找出要求的二面角的平面角,然后通过解直角三角形得到二面角C-BC1-D的正切值.
解答:(1)证明如图,
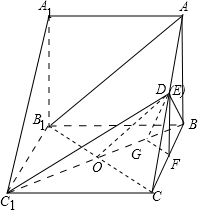
连接B1C,设B1C与BC1相交于点O,连接OD,
∵四边形BCC1B1是平行四边形,
∴点O为B1C的中点.
∵D为AC的中点,∴OD为△AB1C的中位线.∴OD∥AB1.
∵OD?平面BC1D,AB1?平面BC1D,
∴AB1∥平面BC1D;
(2)解:∵AA1⊥平面ABC,AA1?平面AA1C1C,
∴平面ABC⊥平面AA1C1C且平面ABC∩平面AA1C1C=AC.
作BE⊥AC,垂足为E,则BE⊥平面AA1C1C,
∵AA1=AB=2,设BC=x,则AC=A1C1=
,
BE=
,
∴四棱锥B-DAA1C1的体积V=
×
(A1C1+AD)•AA1•BE
=
×
(
+
)×2×
=2.
解得,x=2.
所以D与E重合.
取BC中点F,连结DF,过F作FG⊥BC1与G,连结DG,
则∠DGF为二面角C-BC1-D的平面角.
由△BCC1∽△BGF可求得GF=
.
所以tan∠DGF=
=
=
.

连接B1C,设B1C与BC1相交于点O,连接OD,
∵四边形BCC1B1是平行四边形,
∴点O为B1C的中点.
∵D为AC的中点,∴OD为△AB1C的中位线.∴OD∥AB1.
∵OD?平面BC1D,AB1?平面BC1D,
∴AB1∥平面BC1D;
(2)解:∵AA1⊥平面ABC,AA1?平面AA1C1C,
∴平面ABC⊥平面AA1C1C且平面ABC∩平面AA1C1C=AC.
作BE⊥AC,垂足为E,则BE⊥平面AA1C1C,
∵AA1=AB=2,设BC=x,则AC=A1C1=
| 4+x2 |
BE=
| 2x | ||
|
∴四棱锥B-DAA1C1的体积V=
| 1 |
| 3 |
| 1 |
| 2 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 4+x2 |
| ||
| 2 |
| 2x | ||
|
解得,x=2.
所以D与E重合.
取BC中点F,连结DF,过F作FG⊥BC1与G,连结DG,
则∠DGF为二面角C-BC1-D的平面角.
由△BCC1∽△BGF可求得GF=
| ||
| 2 |
所以tan∠DGF=
| DF |
| GF |
| 1 | ||||
|
| 2 |
点评:本题考查了直线与平面平行的判定,考查了二面角的平面角的求法,综合考查了学生的空间想象能力和思维能力,“寻找垂面,构造垂线”是找二面角平面角的常用方法,此题是中档题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
 如图,直三棱柱ABC-A1B1C1中,
如图,直三棱柱ABC-A1B1C1中, 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点.
如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D为A1C1的中点,E为B1C的中点. 如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是
如图在直三棱柱ABC-A1B1C1中∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是 如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点. 如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.
如图,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中点.