题目内容
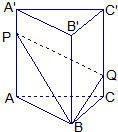如图：直三棱柱ABC-A′B′C′的体积为V，点P、Q分别在侧棱AA′和CC′上，AP=C′Q，则四棱锥B-APQC的体积为分析：四棱锥B-APQC的体积，底面面积是侧面ACC′A′的一半，B到侧面的距离是常数，求解即可．
解答：解：由于四棱锥B-APQC的底面面积是侧面ACC′A′的一半，不妨把P移到A′，Q移到C，
所求四棱锥B-APQC的体积，转化为三棱锥A′-ABC体积，就是：
V
故答案为：
V
所求四棱锥B-APQC的体积，转化为三棱锥A′-ABC体积，就是：
| 1 |
| 3 |
故答案为：
| 1 |
| 3 |
点评：本题考查棱锥的体积，考查转化思想，是基础题．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
新思维寒假作业系列答案
相关题目
如图，直三棱柱ABC-A1B1C1中，
如图，直三棱柱ABC-A1B1C1中，底面是以∠ABC为直角的等腰直角三角形，AC=2a，BB1=3a，D为A1C1的中点，E为B1C的中点．
如图在直三棱柱ABC-A1B1C1中∠ACB=90°，AA1=2，AC=BC=1，则异面直线A1B与AC所成角的余弦值是
如图，直三棱柱ABC-A1B1C1中，AC⊥BC，AC=BC=CC1=2，M，N分别为AC，B1C1的中点．
如图，直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=a，AA1=2a，D棱B1B的中点．