题目内容
 (2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点.
(2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点.(Ⅰ)求证:A1C∥平面AED1;
(Ⅱ)求证:平面AED1⊥平面CDD1.
分析:(I)根据线面平行的判定定理,先证线线平行,再由线线平行证明线面平行即可;
(II)先由线线垂直证线面垂直,再由线面垂直证明面面垂直即可.
(II)先由线线垂直证线面垂直,再由线面垂直证明面面垂直即可.
解答: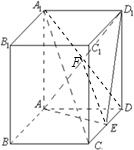 证明:(Ⅰ)连接A1D,交AD1与F,连接EF,
证明:(Ⅰ)连接A1D,交AD1与F,连接EF,
由已知四边形ADD1A1为矩形,∴F为AD1的中点,
又E为CD的中点.∴EF为△AED1的中位线.∴A1C∥EF,
∵A1C?平面AED1,EF?平面AED1,
∴A1C∥平面AED1;
(Ⅱ)由已知DD1⊥AD,DD1⊥BD,
又∵AD∩BD=D,AD?平面ABCD,CD?平面ABCD,
∴DD1⊥平面ABCD,∵AE?平面ABCD,∴AE⊥DD1,
∵底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点.∴AE⊥CD,
又CD∩DD1=D,CD?平面CDD1,DD1?平面CDD1,
∴AE⊥平面CDD1C1,
∵AE?平面AED1,
∴平面AED1⊥平面CDD1.
 证明:(Ⅰ)连接A1D,交AD1与F,连接EF,
证明:(Ⅰ)连接A1D,交AD1与F,连接EF,由已知四边形ADD1A1为矩形,∴F为AD1的中点,
又E为CD的中点.∴EF为△AED1的中位线.∴A1C∥EF,
∵A1C?平面AED1,EF?平面AED1,
∴A1C∥平面AED1;
(Ⅱ)由已知DD1⊥AD,DD1⊥BD,
又∵AD∩BD=D,AD?平面ABCD,CD?平面ABCD,
∴DD1⊥平面ABCD,∵AE?平面ABCD,∴AE⊥DD1,
∵底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点.∴AE⊥CD,
又CD∩DD1=D,CD?平面CDD1,DD1?平面CDD1,
∴AE⊥平面CDD1C1,
∵AE?平面AED1,
∴平面AED1⊥平面CDD1.
点评:本题考查面面垂直的判定、线面平行的判定.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目