题目内容
 如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.(1)求证:无论E在任何位置,都有A1E⊥BD
(2)试确定点E的位置,使得A1-BD-E为直二面角,并说明理由.
(3)试确定点E的位置,使得四面体A1-BDE体积最大.并求出体积的最大值.
分析:(1)由AA1⊥底面ABCD,可得AA1⊥BD,结合菱形的性质可得AC⊥BD,由线面垂直的判定定理可得BD⊥平面AA1C1C,进而得到A1E⊥BD;
(2)由(1)得二面角A1-BD-E的平面角为∠A1OE,令CE=x,利用勾股定理,可得x值,进而确定E点的位置;
(3)过E作A1O的垂线与H,则必有EH⊥平面A1BD,从而dE-A1BD=EH,所以当EH最大时,四面体A1-BDE体积最大.所以当E点和C1重合时体积最大.代入棱锥体积公式,可得答案.
(2)由(1)得二面角A1-BD-E的平面角为∠A1OE,令CE=x,利用勾股定理,可得x值,进而确定E点的位置;
(3)过E作A1O的垂线与H,则必有EH⊥平面A1BD,从而dE-A1BD=EH,所以当EH最大时,四面体A1-BDE体积最大.所以当E点和C1重合时体积最大.代入棱锥体积公式,可得答案.
解答: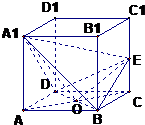 证明:(1)∵AA1⊥底面ABCD,BD?底面ABCD,
证明:(1)∵AA1⊥底面ABCD,BD?底面ABCD,
∴AA1⊥BD
又∵底面ABCD是菱形,
∴AC⊥BD
又∵AA1∩AC=A,AA1,AC?平面AA1C1C
∴BD⊥平面AA1C1C
又∵A1E?平面AA1C1C
∴A1E⊥BD…(4分)
解:(2)由(1)得BD⊥平面AA1C1C,
∴二面角A1-BD-E的平面角为∠A1OE.
令CE=x,则易得A1O=
=
,OE=
=
,
A1E=
=
由A1E2=A1O2+OE2⇒x=
…(8分)
(3)∵VA1-BDE=VE-A1BD=
S△A1BD•dE-A1BD
另一方面,∵BD⊥平面AA1C1C,
∴平面A1BD⊥平面AA1C1C,
过E作A1O的垂线与H,则必有EH⊥平面A1BD,从而dE-A1BD=EH
∴当EH最大时,四面体A1-BDE体积最大.
∴当E点和C1重合时体积最大.此时EH=
,…(11分)
从而VA1-BDE=VE-A1BD=
S△A1BD•dE-A1BD=
…(13分)
 证明:(1)∵AA1⊥底面ABCD,BD?底面ABCD,
证明:(1)∵AA1⊥底面ABCD,BD?底面ABCD,∴AA1⊥BD
又∵底面ABCD是菱形,
∴AC⊥BD
又∵AA1∩AC=A,AA1,AC?平面AA1C1C
∴BD⊥平面AA1C1C
又∵A1E?平面AA1C1C
∴A1E⊥BD…(4分)
解:(2)由(1)得BD⊥平面AA1C1C,
∴二面角A1-BD-E的平面角为∠A1OE.
令CE=x,则易得A1O=
| AA12+AO2 |
| 19 |
| OC2+CE2 |
| x2+3 |
A1E=
| A1C12+C1E2 |
| 12+(4-x)2 |
由A1E2=A1O2+OE2⇒x=
| 3 |
| 4 |
(3)∵VA1-BDE=VE-A1BD=
| 1 |
| 3 |
另一方面,∵BD⊥平面AA1C1C,
∴平面A1BD⊥平面AA1C1C,
过E作A1O的垂线与H,则必有EH⊥平面A1BD,从而dE-A1BD=EH
∴当EH最大时,四面体A1-BDE体积最大.
∴当E点和C1重合时体积最大.此时EH=
8
| ||
| 19 |
从而VA1-BDE=VE-A1BD=
| 1 |
| 3 |
8
| ||
| 3 |
点评:本题考查的知识点是棱锥的体积,直线与平面垂直的性质,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2,四棱锥B-AA1C1D的体积为3.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2,四棱锥B-AA1C1D的体积为3. 如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
