题目内容
 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8.(1)证明:BD⊥EF;
(2)当CF=
| 1 | 4 |
(3)多面体AE-BCFB1的体积V是否为常数?若是,求这个常数,若不是,求V的取值范围.
分析:(1)连接AC,因为ABCD是菱形,所以AC⊥BD,因为ABCD-A1B1C1D1是直四棱柱,所以AA1⊥BD,BD⊥AA1C1C,由此能够证明BD⊥EF.
(2)设AC∩BD=O,以O为原点,AC、BD分别为x轴、y轴建立空间直角坐标系Oxyz,得B(0,-
,0),E(1,0,4)、F(1,0,2),设平面BEF的一个法向量为
=(x,y,z),则
,解得
=(1,-
,1),底面ABCD的一个法向量为
=(0,0,1),由向量法能求出面SEF与底面ABCD所成二面角的大小.
(3)多面体AE-BCFB1是四棱锥B1-AEFC和三棱锥B1-ABC的组合体,依题意,BB1=8,AB=2,BB1是三棱锥B1-ABC的高,BO是四棱锥B1-AEFC的高.由此能求出多面体AE-BCFB1的体积V是常数
.
(2)设AC∩BD=O,以O为原点,AC、BD分别为x轴、y轴建立空间直角坐标系Oxyz,得B(0,-
| 3 |
| n1 |
|
| n1 |
| 3 |
| n2 |
(3)多面体AE-BCFB1是四棱锥B1-AEFC和三棱锥B1-ABC的组合体,依题意,BB1=8,AB=2,BB1是三棱锥B1-ABC的高,BO是四棱锥B1-AEFC的高.由此能求出多面体AE-BCFB1的体积V是常数
16
| ||
| 3 |
解答:(1)证明:连接AC,∵ABCD是菱形,∴AC⊥BD…(1分),
∵ABCD-A1B1C1D1是直四棱柱,AA1⊥面ABCD,BD?面ABCD,
∴AA1⊥BD…(2分),
∵AA1∩AC=A,
∴BD⊥面AA1C1C…(3分),
∵EF?面AA1C1C,
∴BD⊥EF…(4分).
(2)解:设AC∩BD=O,以O为原点,AC、BD分别为x轴、y轴建立空间直角坐标系Oxyz…(5分),
∵直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,侧面展开图是边长为8的正方形,
∴菱形ABCD的边长为2,棱柱侧棱长为8,
所以B(0,-
,0),E(1,0,4)、F(1,0,2)…(6分),
设平面BEF的一个法向量为
=(x,y,z),则
…(7分),
解得
=(1,-
,1)…(8分),
底面ABCD的一个法向量为
=(0,0,1),
设面SEF与底面ABCD所成二面角的大小为θ,
则|cosθ|=
=
,sinθ=
=
.…(9分).
(3)解:多面体AE-BCFB1是四棱锥B1-AEFC和三棱锥B1-ABC的组合体…(10分),
依题意,BB1=8,AB=2…(11分),
BB1是三棱锥B1-ABC的高,BO是四棱锥B1-AEFC的高…(12分),
所以V=
×S△ABC×BB1+
×S△EFC×BO…(13分),
=
是常数…(14分).
∵ABCD-A1B1C1D1是直四棱柱,AA1⊥面ABCD,BD?面ABCD,
∴AA1⊥BD…(2分),
∵AA1∩AC=A,
∴BD⊥面AA1C1C…(3分),
∵EF?面AA1C1C,
∴BD⊥EF…(4分).
(2)解:设AC∩BD=O,以O为原点,AC、BD分别为x轴、y轴建立空间直角坐标系Oxyz…(5分),
∵直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,侧面展开图是边长为8的正方形,
∴菱形ABCD的边长为2,棱柱侧棱长为8,
所以B(0,-
| 3 |
设平面BEF的一个法向量为
| n1 |
|
解得
| n1 |
| 3 |
底面ABCD的一个法向量为
| n2 |
设面SEF与底面ABCD所成二面角的大小为θ,
则|cosθ|=
|
| ||||
|
|
| 1 | ||
|
| 2 | ||
|
2
| ||
| 5 |
(3)解:多面体AE-BCFB1是四棱锥B1-AEFC和三棱锥B1-ABC的组合体…(10分),
依题意,BB1=8,AB=2…(11分),
BB1是三棱锥B1-ABC的高,BO是四棱锥B1-AEFC的高…(12分),
所以V=
| 1 |
| 3 |
| 1 |
| 3 |
=
16
| ||
| 3 |
点评:本题考查两直线垂直的证明、二面角的求法和棱锥体积的计算,考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,是高考的重点,易错点是空间几何知识体系不牢固.解题时要注意向量法的灵活运用.

练习册系列答案
相关题目
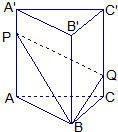 如图:直三棱柱ABC-A′B′C′的体积为V,点P、Q分别在侧棱AA′和CC′上,AP=C′Q,则四棱锥B-APQC的体积为
如图:直三棱柱ABC-A′B′C′的体积为V,点P、Q分别在侧棱AA′和CC′上,AP=C′Q,则四棱锥B-APQC的体积为 如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2.
如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2. (2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点.
(2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点. 如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.