题目内容
椭圆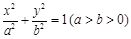 的中心、右焦点、右顶点及右准线与x轴的交点依次为O、F、G、H,则
的中心、右焦点、右顶点及右准线与x轴的交点依次为O、F、G、H,则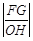 的最大值为( )
的最大值为( )
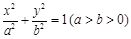 的中心、右焦点、右顶点及右准线与x轴的交点依次为O、F、G、H,则
的中心、右焦点、右顶点及右准线与x轴的交点依次为O、F、G、H,则 的最大值为( )
的最大值为( )A.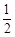 | B. | C. | D.不确定 |
C
依题意得,|FA|即为该椭圆右定点与右焦点间的距离,即|FA|=|OA|-|OF|,
又∵|OA|即为椭圆的长半轴长a,|OF|即为椭圆的半焦距长c,
∴|FA|=a-c.
又∵H为椭圆的右准线与x轴的交点,故|OH|即为椭圆中心到右准线的距离,依准线的定义知,|OH|= ,则
,则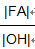 =
= ①
①
又∵椭圆的离心率e= ,(0<e<1),从而c=ae,代入①,得
,(0<e<1),从而c=ae,代入①,得 =
= =e(1-e)=-(e-1/2)2+1/4(0<e<1),
=e(1-e)=-(e-1/2)2+1/4(0<e<1),
当且仅当e=1/2时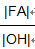 取得最值1/4.
取得最值1/4.
故选择C.
又∵|OA|即为椭圆的长半轴长a,|OF|即为椭圆的半焦距长c,
∴|FA|=a-c.
又∵H为椭圆的右准线与x轴的交点,故|OH|即为椭圆中心到右准线的距离,依准线的定义知,|OH|=
 ,则
,则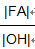 =
= ①
①又∵椭圆的离心率e=
 ,(0<e<1),从而c=ae,代入①,得
,(0<e<1),从而c=ae,代入①,得 =
= =e(1-e)=-(e-1/2)2+1/4(0<e<1),
=e(1-e)=-(e-1/2)2+1/4(0<e<1),当且仅当e=1/2时
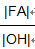 取得最值1/4.
取得最值1/4.故选择C.

练习册系列答案
相关题目
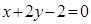 交椭圆于A、B两点,线段AB的中点为M(1,
交椭圆于A、B两点,线段AB的中点为M(1,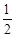 ),
),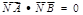 ,求动点N的轨迹方程。
,求动点N的轨迹方程。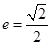 ,椭圆上的点到焦点的最短距离为
,椭圆上的点到焦点的最短距离为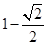 , 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且
, 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且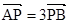 .
.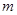 的取值范围.
的取值范围.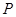 是椭圆
是椭圆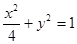 与双曲线
与双曲线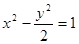 的一个交点,
的一个交点,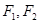 是椭圆的左右焦点,则
是椭圆的左右焦点,则 .
. 的共同焦点为
的共同焦点为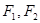 ,
,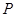 是两曲线的一个交点,则
是两曲线的一个交点,则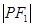 ·
· 的值为______________.
的值为______________.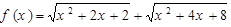 的最小值为( )
的最小值为( )



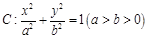 的离心率为
的离心率为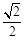 ,其中左焦点
,其中左焦点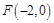
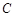 的方程
的方程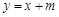 与椭圆
与椭圆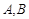 ,且线段
,且线段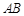 的中
的中 点
点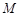 关于直线
关于直线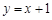 的对称点在圆
的对称点在圆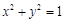 上,求
上,求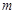 的值
的值 ,则椭圆的离心率的取值范围是( )
,则椭圆的离心率的取值范围是( )



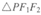 的一个顶点P(7,12)在双曲线
的一个顶点P(7,12)在双曲线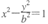 上,另外两顶点F1、F2为该双曲线的左、右焦点,则
上,另外两顶点F1、F2为该双曲线的左、右焦点,则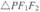 的内心坐标为____
的内心坐标为____