题目内容
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,点
,点![]() 分别为椭圆
分别为椭圆![]() 与坐标轴的交点,且
与坐标轴的交点,且![]() .过
.过![]() 轴上定点
轴上定点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 为线段
为线段![]() 的中点.
的中点.
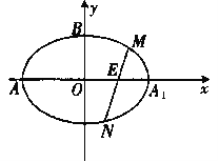
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由题设知椭圆的离心率和![]() 的关系,结合
的关系,结合![]() ,求得
,求得![]() 的值,即可得到椭圆的标准方程;
的值,即可得到椭圆的标准方程;
(2)分直线MN的斜率为0和不为0两种情况讨论,设直线MN的方程与椭圆的方程联立,结合根与系数的关系,求得点Q的坐标,得出点Q到AB的距离,求得面积的表达式,利用基本不等式,即可求解.
(1)由题意,椭圆![]() 的离心率为
的离心率为![]() ,所以
,所以![]() ,
,
其中![]() ,
,![]() ,
,
由![]() ,得
,得![]() .
.
又由![]() ,得
,得![]() ,
,![]() ,
,![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)直线![]() 的方程为
的方程为![]() ,
,
①当直线![]() 的斜率
的斜率![]() 时,直线过点
时,直线过点![]() 交椭圆于左右顶点,则中点为坐标原点
交椭圆于左右顶点,则中点为坐标原点![]() ,此时
,此时![]() ,
,
②当直线![]() 的斜率
的斜率![]() 时,设直线的方程为
时,设直线的方程为![]() ,
,
联立方程组 ,得
,得![]() ,∴点
,∴点![]() 为
为![]() ,
,
∴点![]() 到直线
到直线![]() 的距离
的距离![]() 为
为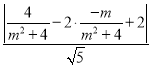 ,
,
∵点![]() 在直线
在直线![]() 的下方,即
的下方,即![]() ,
,
∴ ,
,
∴ ,
,
设![]() ,令
,令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时, ,
,
当且仅当![]() ,即
,即![]() 时等号成立,此时
时等号成立,此时 ,
,
当![]() 时,
时,![]() ,此时
,此时![]() ,
,
综上所述,![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目