题目内容
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() ,侧棱
,侧棱![]() 底面
底面![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,作
的中点,作![]() ,交
,交![]() 于点
于点![]() .
.
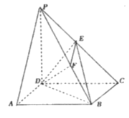
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() ;
;
(3)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)见解析 (3)![]()
【解析】
(1)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,根据中位线定理证明
,根据中位线定理证明![]() ,即可证得
,即可证得![]() 平面
平面![]() .
.
(2)先证![]() 平面
平面![]() .又∵
.又∵![]() 平面
平面![]() ,则
,则![]() .
.
(3)建立空间直角坐标系,列出各点的坐标表示,求出平面![]() 的法向量为
的法向量为![]() ,又因
,又因![]() 平面
平面![]() ,所以
,所以![]() 为平面
为平面![]() 的一条法向量,利用余弦公式求解即可得出二面角
的一条法向量,利用余弦公式求解即可得出二面角![]() 的余弦值.
的余弦值.
解:(1)证明:连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
因为![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,所以
的中点,所以![]() 为
为![]() 的中位线
的中位线
∴![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]()
(2)在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,
的中点,
∴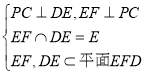 ,则
,则![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,则
,则![]() .
.
(3)取![]() 中点
中点![]() ,连接
,连接![]() .
.
依题意可得![]() 为等边三角形,∴
为等边三角形,∴![]() ,
,![]()
又因为![]() 底面
底面![]() ,
,![]() ,
,![]() 平面
平面![]()
则![]() ,
,![]()
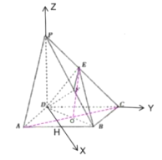
建立以![]() 为坐标原点,如图所示坐标系,则有:
为坐标原点,如图所示坐标系,则有:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,
,
则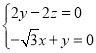
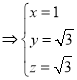 ,∴
,∴![]()
∵![]() 平面
平面![]() ,所以
,所以![]() 为平面
为平面![]() 的一条法向量,且
的一条法向量,且![]()
∴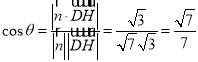

练习册系列答案
相关题目
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元.在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费.现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
记![]() 表示1台机器在三年使用期内的维修次数,
表示1台机器在三年使用期内的维修次数,![]() 表示1台机器在维修上所需的费用(单位:元),
表示1台机器在维修上所需的费用(单位:元),![]() 表示购机的同时购买的维修服务次数.
表示购机的同时购买的维修服务次数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)若要求“维修次数不大于![]() ”的频率不小于0.8,求
”的频率不小于0.8,求![]() 的最小值.
的最小值.