题目内容
【题目】在平面四边形
中，
、
分
、
所成的比为
，即
，则有：
.
（1）拓展到空间，写出空间四边形类似的命题，并加以证明；
（2）在长方体
中，
，
，
，、分别为
、
的中点，利用上述（1）的结论求线段
的长度；
（3）在所有棱长均为
平行六面体中，
（
为锐角定值），、分
、
所成的比为，求的长度.（用，，表示）
【答案】（1）命题同题干，证明见解析；（2）
；（3）
【解析】
（1）由条件可得
，利用向量的线性运算证明即可；
（2）由（1）的结论可得
，两边同时平方计算可得结果；
（3）由（1）的结论可得
，两边同时平方计算可得结果.
（1）在空间四边形
中，
、
分
、
所成的比为
，即
，则有：.
证明：
；
（2）由（1）的结论可得
，
，
；
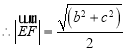（3）如图：
与
所成的角为
，
又由（1）的结论可得，
，
.
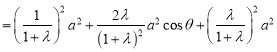
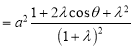七星图书口算速算天天练系列答案【题目】某商场举行有奖促销活动，顾客购买一定金额的商品后即可参加一次抽奖.随着抽奖活动的有效开展，参与抽奖活动的人数越来越多，该商场对前5天抽奖活动的人数进行统计，y表示第x天参加抽奖活动的人数，得到统计表如下：
x | 1 | 2 | 3 | 4 | 5 |
y | 50 | 60 | 70 | 80 | 100 |
经过进一步统计分析，发现y与x具有线性相关关系.
（1）若从这5天随机抽取两天，求至少有1天参加抽奖人数超过70的概率；
（2）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
，并估计该活动持续7天，共有多少名顾客参加抽奖？
参考公式及数据：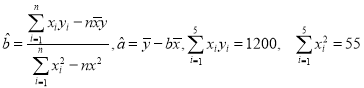
.
【题目】某小区所有263户家庭人口数分组表示如下：
家庭人口数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
家庭数 | 20 | 29 | 48 | 50 | 46 | 36 | 19 | 8 | 4 | 3 |
（1）若将上述家庭人口数的263个数据分布记作
，平均值记作
，写出人口数方差的计算公式（只要计算公式，不必计算结果）；
（2）写出他们家庭人口数的中位数（直接给出结果即可）；
（3）计算家庭人口数的平均数与标准差.（写出公式，再利用计算器计算，精确到0.01）
