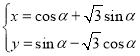题目内容
【题目】已知点![]() ,动点
,动点![]() 到直线
到直线![]() 的距离与动点
的距离与动点![]() 到点
到点![]() 的距离之比为
的距离之比为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作任一直线交曲线
作任一直线交曲线![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 的垂线交直线
的垂线交直线![]() 于点
于点![]() ,求证:
,求证:![]() 平分线段
平分线段![]() .
.
【答案】(1)![]() (2)见证明
(2)见证明
【解析】
(1)由动点![]() 到直线
到直线![]() 的距离与动点
的距离与动点![]() 到点
到点![]() 的距离之比为
的距离之比为![]() ,列出方程,即可求解;
,列出方程,即可求解;
(2)设![]() 的直线方程为
的直线方程为![]() ,得
,得![]() 的直线方程为
的直线方程为![]() ,分别与直线
,分别与直线![]() 和椭圆的方程联立方程组,利用根与系数的关系求得
和椭圆的方程联立方程组,利用根与系数的关系求得![]() ,
,![]() 的坐标,将点
的坐标,将点![]() 坐标代入直线
坐标代入直线![]() 的方程,即可得到结论.
的方程,即可得到结论.
(1)设![]() ,由动点
,由动点![]() 到直线
到直线![]() 的距离与动点
的距离与动点![]() 到点
到点![]() 的距离之比为
的距离之比为![]() ,
,
则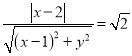 ,化简得
,化简得![]() .
.
(2)设![]() 的直线方程为
的直线方程为![]() ,则
,则![]() 的直线方程为
的直线方程为![]() ,
,
联立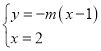 ,解得
,解得![]() ,∴直线
,∴直线![]() 的方程为
的方程为![]() ,
,
联立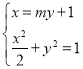 得
得![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,
设![]() 的中点为
的中点为![]() ,则
,则![]() ,
,
∴![]() ,∴
,∴![]() ,
,
将点![]() 坐标代入直线
坐标代入直线![]() 的方程
的方程![]() ,
,
∴点![]() 在直线
在直线![]() 上,∴
上,∴![]() 平分线段
平分线段![]() .
.

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
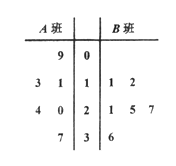
课堂小作业系列答案【题目】诚信是立身之本,道德之基,某校学生会创设了“诚信水站”,既便于学生用水,又推进诚信教育,并用“![]() ”表示每周“水站诚信度”,为了便于数据分析,以四周为一周期,下表为该水站连续十二周(共三个周期)的诚信数据统计:
”表示每周“水站诚信度”,为了便于数据分析,以四周为一周期,下表为该水站连续十二周(共三个周期)的诚信数据统计:
第一周 | 第二周 | 第三周 | 第四周 | |
第一个周期 |
|
|
|
|
第二个周期 |
|
|
|
|
第三个周期 |
|
|
|
|
(1)计算表中十二周“水站诚信度”的平均数![]() ;
;
(2)分别从表中每个周期的4个数据中随机抽取1个数据,设随机变量![]() 表示取出的3个数中“水站诚信度”超过
表示取出的3个数中“水站诚信度”超过![]() 的数据的个数,求随机变量
的数据的个数,求随机变量![]() 的分布列和期望;
的分布列和期望;
(3)已知学生会分别在第一个周期的第四周末和第二个周期的第四周末各举行了一次“以诚为本”的主题教育活动,根据已有数据,说明两次主题教育活动的宣传效果,并根据已有数据陈述理由.
【题目】某企业购买某种仪器,在仪器使用期间可能出现故障,需要请销售仪器的企业派工程师进行维修,因为考虑到人力、成本等多方面的原因,销售仪器的企业提供以下购买仪器维修服务的条件:在购买仪器时,可以直接购买仪器维修服务,维修一次1000元;在仪器使用期间,如果维修服务次数不够再次购买,则需要每次1500元..现需决策在购买仪器的同时购买几次仪器维修服务,为此搜集并整理了500台这种机器在使用期内需要维修的次数,得到如下表格:
维修次数 | 5 | 6 | 7 | 8 | 9 |
频数(台) | 50 | 100 | 150 | 100 | 100 |
记![]() 表示一台仪器使用期内维修的次数,
表示一台仪器使用期内维修的次数,![]() 表示一台仪器使用期内维修所需要的费用,
表示一台仪器使用期内维修所需要的费用,![]() 表示购买仪器的同时购买的维修服务的次数.
表示购买仪器的同时购买的维修服务的次数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)以这500台仪器使用期内维修次数的频率代替一台仪器维修次数发生的概率,求![]() 的概率.
的概率.
(3)假设购买这500台仪器的同时每台都购买7次维修服务,或每台都购买8次维修服务,请分别计算这500台仪器在购买维修服务所需要费用的平均数,以此为决策依据,判断购买7次还是8次维修服务?