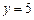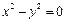题目内容
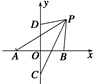
如图所示,线段AB与CD互相垂直平分于点O,|AB|=2a(a>0),|CD|="2b" (b>0),动点P满足|PA|·|PB|=|PC|·|PD|.求动点P的轨迹方程.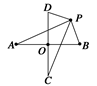

P的轨迹方程为x2-y2=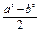
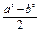
以O为坐标原点,直线AB、CD分别为x轴、y轴建立直角坐标系,
则A(-a,0),B(a,0),C(0,-b),D(0,b),
设P(x,y),由题意知|PA|·|PB|=|PC|·|PD|,
∴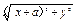 ·
·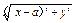
=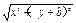 ·
·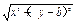 ,
,
化简得x2-y2=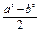 .
.
故动点P的轨迹方程为x2-y2=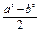 .
.
则A(-a,0),B(a,0),C(0,-b),D(0,b),

设P(x,y),由题意知|PA|·|PB|=|PC|·|PD|,
∴
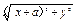 ·
·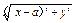
=
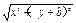 ·
·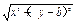 ,
,化简得x2-y2=
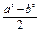 .
.故动点P的轨迹方程为x2-y2=
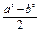 .
.
练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 的左、右焦点分别为
的左、右焦点分别为 、
、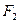 ,其中
,其中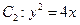 的焦点,
的焦点,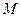 是
是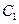 与
与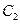 在第一象限的交点,且
在第一象限的交点,且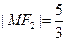 .(Ⅰ)求椭圆
.(Ⅰ)求椭圆 的顶点A﹑C在椭圆
的顶点A﹑C在椭圆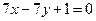 上,求直线
上,求直线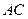 的方程.
的方程.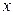 轴上,离心率
轴上,离心率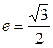 ,已知点
,已知点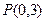 到这个椭圆上的点的最远距离是4,求这个椭圆的方程.
到这个椭圆上的点的最远距离是4,求这个椭圆的方程.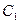 :
: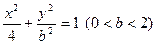 的离心率等于
的离心率等于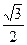 ,抛物线
,抛物线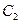 :
: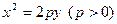 的焦点在椭圆的顶点上。(Ⅰ)求抛物线
的焦点在椭圆的顶点上。(Ⅰ)求抛物线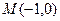 的直线
的直线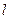 与抛物线
与抛物线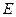 、
、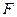 两点,又过
两点,又过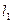 、
、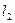 ,当
,当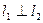 时,求直线
时,求直线 (-4,0)、F
(-4,0)、F (4,0),并且椭圆和长轴长是双曲线实轴长的2倍,试求椭圆与双曲线交点的轨迹方程。
(4,0),并且椭圆和长轴长是双曲线实轴长的2倍,试求椭圆与双曲线交点的轨迹方程。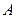 的坐标是
的坐标是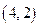 ,底边一个端点
,底边一个端点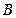 的坐标是
的坐标是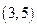 ,求另一个端点
,求另一个端点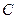 的轨迹方程,并说明它是什么图形.
的轨迹方程,并说明它是什么图形.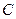 的中心在原点
的中心在原点 ,焦点在
,焦点在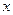 轴上,右准线的方程为
轴上,右准线的方程为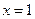 ,倾斜角为
,倾斜角为 的直线
的直线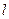 交椭圆
交椭圆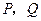 两点,且
两点,且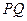 的中点坐标为
的中点坐标为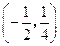 ,求椭圆
,求椭圆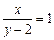 表示斜率为1,在
表示斜率为1,在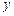 轴上的截距为2的直线
轴上的截距为2的直线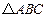 三个顶点的坐标是
三个顶点的坐标是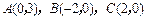 ,中线
,中线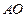 的方程是
的方程是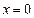
 轴距离为5的点的轨迹方程是
轴距离为5的点的轨迹方程是