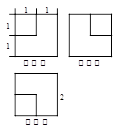题目内容
我国齐梁时代的数学家祖暅(公元5-6世纪)提出了一条原理:“幂势既同,则积不容异.”这句话的意思是:夹在两个平行平面间的两个几何体,被平行于这两个平行平面的任何平面所截,如果截得的两个截面的面积总是相等,那么这两个几何体的体积相等.
设:由曲线 和直线
和直线 ,
, 所围成的平面图形,绕
所围成的平面图形,绕 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为 ;由同时满足
;由同时满足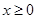 ,
, ,
, ,
, 的点
的点 构成的平面图形,绕
构成的平面图形,绕 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为 .根据祖暅原理等知识,通过考察
.根据祖暅原理等知识,通过考察 可以得到
可以得到 的体积为
的体积为
设:由曲线
 和直线
和直线 ,
, 所围成的平面图形,绕
所围成的平面图形,绕 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为 ;由同时满足
;由同时满足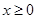 ,
, ,
, ,
, 的点
的点 构成的平面图形,绕
构成的平面图形,绕 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为 .根据祖暅原理等知识,通过考察
.根据祖暅原理等知识,通过考察 可以得到
可以得到 的体积为
的体积为 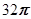
试题分析:根据题意,由于满足
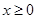 ,
, ,
, ,
, 的点
的点 构成的平面图形,绕
构成的平面图形,绕 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为 ,可知围成的面积为圆内的两个对称的部分,可知得到两个这样的面积的曲边梯形,且面积为
,可知围成的面积为圆内的两个对称的部分,可知得到两个这样的面积的曲边梯形,且面积为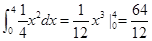 ,绕着y轴旋转得到的是两个圆锥的体积,那可知得到体积为
,绕着y轴旋转得到的是两个圆锥的体积,那可知得到体积为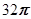 ,那么根据祖暅原理可知,夹在两个平行平面间的两个几何体,被平行于这两个平行平面的任何平面所截,如果截得的两个截面的面积总是相等
,那么根据祖暅原理可知,夹在两个平行平面间的两个几何体,被平行于这两个平行平面的任何平面所截,如果截得的两个截面的面积总是相等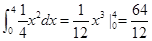 ,那么这两个几何体的体积相等,即可知由曲线
,那么这两个几何体的体积相等,即可知由曲线 和直线
和直线 ,
, 所围成的平面图形,绕
所围成的平面图形,绕 轴旋转一周所得到的旋转体为
轴旋转一周所得到的旋转体为 为
为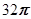 ,故答案为
,故答案为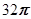 。
。点评:主要是考查了类比推理的运用,属于中档题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
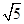 ,球面上有A、B、C三点,如果
,球面上有A、B、C三点,如果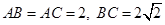 ,则三棱锥O-ABC 的体积为 ( )
,则三棱锥O-ABC 的体积为 ( )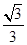 (B)
(B)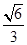 (C)1 (D)
(C)1 (D)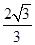
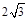 ,则其外接球的表面积为 .
,则其外接球的表面积为 .  ,求其直径
,求其直径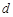 的一个近似公式
的一个近似公式 . 人们还用过一些类似的近似公式. 根据
. 人们还用过一些类似的近似公式. 根据 判断,下列近似公式中最精确的一个是( )
判断,下列近似公式中最精确的一个是( )