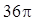题目内容
设三棱锥3个侧面两两互相垂直,且侧棱长均为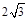 ,则其外接球的表面积为 .
,则其外接球的表面积为 .
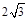 ,则其外接球的表面积为 .
,则其外接球的表面积为 . 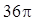
试题分析:根据题意,由于三棱锥3个侧面两两互相垂直,且侧棱长均为
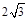 ,可以转化为长方体的一个角,那么其外接球半径就是棱长为
,可以转化为长方体的一个角,那么其外接球半径就是棱长为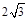 的正方体的外接球的半径,故为3,那么可知球的表面积公式为
的正方体的外接球的半径,故为3,那么可知球的表面积公式为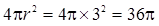 ,故答案为
,故答案为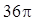
点评:主要是考查了棱锥的外接球的表面积的求解,属于基础题。

练习册系列答案
相关题目
题目内容
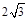 ,则其外接球的表面积为 .
,则其外接球的表面积为 . 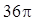
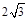 ,可以转化为长方体的一个角,那么其外接球半径就是棱长为
,可以转化为长方体的一个角,那么其外接球半径就是棱长为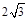 的正方体的外接球的半径,故为3,那么可知球的表面积公式为
的正方体的外接球的半径,故为3,那么可知球的表面积公式为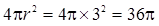 ,故答案为
,故答案为