��Ŀ����
��ƽ��㼯M���㣺����㣨x��y����M������t�ʣ�0��+�ޣ������У�tx��ty����M����Ƹõ㼯M�ǡ�t���ȶ����㼯�������ĸ����⣺
�ٶ�����ƽ��㼯M������������t��ʹ��M�ǡ�t���ȶ����㼯��
����M={��x��y��|x2��y}����M�ǡ�
���ȶ����㼯��
����M={��x��y��|x2+y2+2x+4y=0}����M�ǡ�2���ȶ����㼯��
����M={��x��y��|x2+2y2��1}���ǡ�t���ȶ����㼯����t��ȡֵ��Χ�ǣ�0��1]��
������ȷ��������Ϊ��������
�ٶ�����ƽ��㼯M������������t��ʹ��M�ǡ�t���ȶ����㼯��
����M={��x��y��|x2��y}����M�ǡ�
| 1 |
| 2 |
����M={��x��y��|x2+y2+2x+4y=0}����M�ǡ�2���ȶ����㼯��
����M={��x��y��|x2+2y2��1}���ǡ�t���ȶ����㼯����t��ȡֵ��Χ�ǣ�0��1]��
������ȷ��������Ϊ��������
| A���٢� | B���ڢ� | C���٢� | D���ۢ� |
���㣺Ԫ���뼯�Ϲ�ϵ���ж�,���мĺ�������
ר�⣺����
���������ȣ����ڢ٣�ֱ���жϼ��ɣ����ڢڣ�ȡ��2��3����������֤���ɣ����ڢۣ�ȡ��1��-1����֤���ɣ����ڢܣ���ֱ�Ӹ��ݡ�t���ȶ����㼯������⣮
����⣺���ڢ٣�ƽ��㼯M={��x��y��|x��y��R}��
�ࣨtx��ty����M��
�����ȷ��
���ڢڣ���M={��x��y��|x2��y}��
��ȡ��2��3����
���㣨1��
��∉M��
��ڴ���
���ڢۣ�ȡ��1��-1��Ϊ����M�ϵ�һ�㣬
��2��-2��∉M��
��۴���
���ڢܣ���x2+2y2��1���������⣬��
��t2��x2+2y2����1��
��t�ʣ�0��+�ޣ���
��t�ʣ�0��1]��
�����ȷ��
��ѡ��C
�ࣨtx��ty����M��
�����ȷ��
���ڢڣ���M={��x��y��|x2��y}��
��ȡ��2��3����
���㣨1��
| 3 |
| 2 |
��ڴ���
���ڢۣ�ȡ��1��-1��Ϊ����M�ϵ�һ�㣬
��2��-2��∉M��
��۴���
���ڢܣ���x2+2y2��1���������⣬��
��t2��x2+2y2����1��
��t�ʣ�0��+�ޣ���
��t�ʣ�0��1]��
�����ȷ��
��ѡ��C
�����������ص㿼���˼��ϵ�Ԫ��������������Ϣ�����⣬�Ѷ��еȣ�ȷ�����������Ϣ�ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
�輯��A={1��2��4}������B={x|x=a+b��a��A��b��A}����B���У���������Ԫ�أ�
| A��4 | B��5 | C��6 | D��7 |
����A��B����A��B={1��2}����ͬ�����϶ԣ�A��B�����У�������
| A��4�� | B��7�� | C��8�� | D��9�� |
��Ԫ��1��2��3��ɵļ��Ͽɼ�Ϊ��������
| A��{x=1��2��3} | B��{x=1��x=2��x=3} | C��{x|x��N+��x��4} | D��{6��������} |
����ʽax��b�Ľ⼯�������ǣ�������
| A��∅ | ||
| B��R | ||
C����
| ||
D����-�ޣ�-
|
��֪����A={x|-1��x��0}��B={x|x��a}����A⊆B����ʵ��a��ȡֵ��ΧΪ��������
| A����-�ޣ�0] | B��[0��+�ޣ� | C����-�ޣ�0�� | D����0��+�ޣ� |
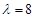 ����Ӧ��һ����������
����Ӧ��һ����������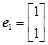 �����Ҿ���M��Ӧ�ı任����
�����Ҿ���M��Ӧ�ı任����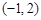 �任��
�任��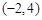 ,�����M��.
,�����M��.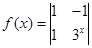 ����
����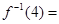 ��
��