题目内容
不等式ax＞b的解集不可能是（ ）
| A、∅ | ||
| B、R | ||
C、（
| ||
D、（-∞，-
|
考点：集合的表示法
专题：不等式的解法及应用,集合
分析：对a 的情况进行分析，得到可能的解．
解答：解：当a=0，b＜0时，不等式ax＞b的解集为R；当a=0，b≥0时，不等式ax＞b的解集为∅；
当a＞0，根据一元一次不等式的解法，两边同除以a得到不等式ax＞b的解集为x＞
；解集为C；
当a＜0时，根据一元一次不等式的解法，不等式两边同除以a，得到不等式ax＞b的解集为x＜
；
所以不等式ax＞b的解集不可能为D；
故选D．
当a＞0，根据一元一次不等式的解法，两边同除以a得到不等式ax＞b的解集为x＞
| b |
| a |
当a＜0时，根据一元一次不等式的解法，不等式两边同除以a，得到不等式ax＞b的解集为x＜
| b |
| a |
所以不等式ax＞b的解集不可能为D；
故选D．
点评：本题考查了一次不等式的解法，要注意一次项的系数．
练习册系列答案
阅读快车系列答案
相关题目
设集合N={x|x2≤x}，则N=（ ）
| A、{0，1} | B、[0，1] | C、（0，1） | D、[0，1） |
下列五种表示法：
①{x=2，y=1}；
②{（x，y）|
}；
③{（2，1）}；
④{2，1}；
⑤{（x，y）|x=2或y=1}；
能正确表示方程组
的解集是（ ）
①{x=2，y=1}；
②{（x，y）|
|
③{（2，1）}；
④{2，1}；
⑤{（x，y）|x=2或y=1}；
能正确表示方程组
|
| A、①②③④⑤ | B、②③④ |
| C、②③ | D、②③⑤ |
若集合A={x∈R|x-4|≤2}，非空集合B={x∈R|2a≤x≤a+3}，若B⊆A，则实数a的取值范围是（ ）
| A、（3，+∞） | B、[-1，+∞） | C、（1，3） | D、[1，3] |
：
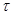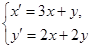对应的矩阵为
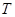，向量β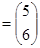
．
；
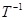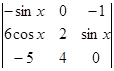
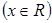中元素4的代数余子式的值记为
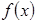，则函数
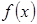的最小值为