题目内容
集合A,B满足A∪B={1,2},则不同的有序集合对(A,B)共有( )
| A、4个 | B、7个 | C、8个 | D、9个 |
考点:元素与集合关系的判断
专题:集合
分析:由已知中集合A,B满足A∪B={1,2},列举出所有满足条件的有序集合对(A,B),可得答案.
解答:解:∵A∪B={1,2},则A,B均为{1,2}的子集,
即A,B∈{∅,{1},{2},{1,2}},
当A=∅时,B={1,2},
当A={1}时,B={1,2}或B={2},
当A={2}时,B={1,2}或B={1},
A={1,2}时,B={1,2},或B={1},或B={2},或B=∅,
共9种情况,
故选:D
即A,B∈{∅,{1},{2},{1,2}},
当A=∅时,B={1,2},
当A={1}时,B={1,2}或B={2},
当A={2}时,B={1,2}或B={1},
A={1,2}时,B={1,2},或B={1},或B={2},或B=∅,
共9种情况,
故选:D
点评:本题考查的知识点是集合的包含关系,其中分析出A,B均为{1,2}的子集,进而列举出所有情况是解答的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
对于任意两个正整数m,n,定义某种运算?:当m,n都为偶数或奇数时,m?n=m+n;当m,n中一个为奇数,另一个为偶数时,m?n=m•n.则在上述定义下,集合M={(x,y)|x?y=36,x∈N*,y∈N*}中元素的个数为( )
| A、48 | B、41 | C、40 | D、39 |
设集合N={x|x2≤x},则N=( )
| A、{0,1} | B、[0,1] | C、(0,1) | D、[0,1) |
已知M={a||a|≥2},A={a|(a-2)(a2-3)=0,a∈M}则集合A的子集共有( )
| A、1个 | B、2个 | C、4个 | D、8 个 |
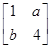 对应的变换作用下得到直线m:x-y-4=0,求实数a,b的值.
对应的变换作用下得到直线m:x-y-4=0,求实数a,b的值.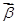 =
=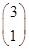 ,变换T的矩阵为A=
,变换T的矩阵为A=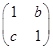 ,平面上的点P(1,1)在变换T作用下得到点P′(3,3),求A-1
,平面上的点P(1,1)在变换T作用下得到点P′(3,3),求A-1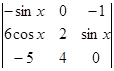
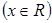 中元素4的代数余子式的值记为
中元素4的代数余子式的值记为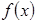 ,则函数
,则函数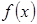 的最小值为
的最小值为