题目内容
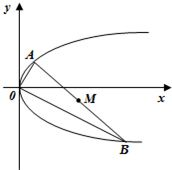
以抛物线y2=4x的焦点为右焦点的椭圆,上顶点为B2,右顶点为A2,左、右焦点为F1、F2,且|
|cos∠B2F1F2=
|
|,过点D(0,2)的直线l,斜率为k(k>0),l与椭圆交于M,N两点.
(1)求椭圆的标准方程;
(2)若M,N的中点为H,且
∥
,求出斜率k的值;
(3)在x轴上是否存在点Q(m,0),使得以QM,QN为邻边的四边形是个菱形?如果存在,求出m的范围;否则,请说明理由.
| F1B2 |
| ||
| 3 |
| OB2 |
(1)求椭圆的标准方程;
(2)若M,N的中点为H,且
| OH |
| A2B2 |
(3)在x轴上是否存在点Q(m,0),使得以QM,QN为邻边的四边形是个菱形?如果存在,求出m的范围;否则,请说明理由.
(1)抛物线y2=4x的焦点为(1,0),∴椭圆中c=1,
∵|
|cos∠B2F1F2=
|
|,
∴b=
c=
,
∴a=2,
∴椭圆的标准方程为
+
=1;
(2)设l:y=kx+2(k>0),M(x1,y1),N(x2,y2),
直线代入椭圆方程得(4k2+3)x2+16kx+4=0,
∴△=12k2-3>0,
∵k>0,∴k>
,
且x1+x2=
,x1x2=
,
∴MN的中点H(
,
),
∵
∥
,
∴
=
,
∴k=
>
,
∴k=
;
(3)设在x轴上存在点Q(m,0),使得以QM,QN为邻边的四边形是个菱形,则HQ⊥MN,
∴
•k=-1,
∴m=-
=-
≥-
=-
,
当且仅当4k=
,即k=
时取等号,
又m=-
<0,
∴在x轴上存在点Q(m,0),使得以QM,QN为邻边的四边形是个菱形,m范围是[-
,0).
∵|
| F1B2 |
| ||
| 3 |
| OB2 |
∴b=
| 3 |
| 3 |
∴a=2,
∴椭圆的标准方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)设l:y=kx+2(k>0),M(x1,y1),N(x2,y2),
直线代入椭圆方程得(4k2+3)x2+16kx+4=0,
∴△=12k2-3>0,
∵k>0,∴k>
| 1 |
| 2 |
且x1+x2=
| -16k |
| 4k2+3 |
| 4 |
| 4k2+3 |
∴MN的中点H(
| -8k |
| 4k2+3 |
| 6 |
| 4k2+3 |
∵
| OH |
| A2B2 |
∴
| ||
|
| ||
| 0-2 |
∴k=
| ||
| 2 |
| 1 |
| 2 |
∴k=
| ||
| 2 |
(3)设在x轴上存在点Q(m,0),使得以QM,QN为邻边的四边形是个菱形,则HQ⊥MN,
∴
| ||
|
∴m=-
| 2k |
| 4k2+3 |
| 2 | ||
4k+
|
| 2 | ||||
2
|
| ||
| 6 |
当且仅当4k=
| 3 |
| k |
| ||
| 2 |
又m=-
| 2k |
| 4k2+3 |
∴在x轴上存在点Q(m,0),使得以QM,QN为邻边的四边形是个菱形,m范围是[-
| ||
| 6 |

练习册系列答案
相关题目