题目内容
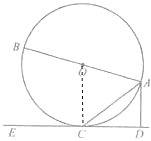
【题目】如图,已知AB是⊙O的直径,AC是弦,AD⊥CE,垂足为D,AC平分∠BAD.
(1)求证:直线CE是⊙O的切线;
(2)求证:AC2=ABAD.
【答案】
(1)证明:连接OC,如下图所示:
因为OA=OC,
所以∠OCA=∠OAC.
又因为AD⊥CE,
所以∠ACD+∠CAD=90°,
又因为AC平分∠BAD,
所以∠OCA=∠CAD,
所以∠OCA+∠CAD=90°,
即OC⊥CE,
所以CE是⊙O的切线.
(2)证明:连接BC,
因为AB是⊙O的直径,
所以∠BCA=∠ADC=90°,
因为CE是⊙O的切线,
所以∠B=∠ACD,
所以△ABC∽△ACD,
所以 ![]() ,
,
即AC2=ABAD.
【解析】(1)连接OC,利用△OAC为等腰三角形,结合同角的余角相等,我们易结合AD⊥CE,得到OC⊥DE,根据切线的判定定理,我们易得到结论;(2)连接BC,我们易证明△ABC∽△ACD,然后相似三角形性质,相似三角形对应边成比例,易得到结论.

练习册系列答案
相关题目


