题目内容
设二次函数f(x)=ax2+bx+c(a,b,c∈R)满足下列条件:①当x∈R时,f(x)的最小值为0,且图象关于直线x=-1对称;
②当x∈(0,5)时,x≤f(x)≤2|x-1|+1恒成立.
(1)求f(1)的值;
(2)求函数f(x)的解析式;
(3)若f(x)在区间[m-1,m]上恒有|f(x)-x|≤1,求实数m的取值范围.
【答案】分析:(1)由“当x∈(0,5)时,x≤f(x)≤2|x-1|+1恒成立”得到当x=1时,也成立,所以有1≤f(1)≤1,
从而得到f(1);
(2)由“当x∈R时,f(x)的最小值为0,且图象关于直线x=-1对称”,可知对称轴及在对称轴处取得最值,创造两个条件,再由f(1)=1,可求得二次函数的解析式.
(3)根据第二问可设:g(x)=f(x)-x=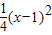 ,由“|f(x)-x|≤1”可得x∈[-1,3],从而求得结论.
,由“|f(x)-x|≤1”可得x∈[-1,3],从而求得结论.
解答:解:(1)∵当x∈(0,5)时,x≤f(x)≤2|x-1|+1恒成立
∴1≤f(1)≤1
∴f(1)=1;
(2)∵当x∈R时,f(x)的最小值为0,且图象关于直线x=-1对称;
∴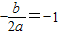 ,f(-1)=a-b+c=0
,f(-1)=a-b+c=0
又∵f(1)=a+b+c=1
∴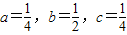
∴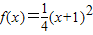 ;
;
(3)设g(x)=f(x)-x=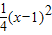
关于x=1对称
当x∈[-1,3]时,|f(x)-x|≤1
∴0≤m≤3.
点评:本题主要考查二次函数求解析式,里面有三个未知数所以要寻求三个条件来解,同时还考查了用二次函数构造新函数来研究恒成立问题,二次函数渗透性强,应用范围广,图象和性质要灵活掌握.
从而得到f(1);
(2)由“当x∈R时,f(x)的最小值为0,且图象关于直线x=-1对称”,可知对称轴及在对称轴处取得最值,创造两个条件,再由f(1)=1,可求得二次函数的解析式.
(3)根据第二问可设:g(x)=f(x)-x=
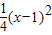 ,由“|f(x)-x|≤1”可得x∈[-1,3],从而求得结论.
,由“|f(x)-x|≤1”可得x∈[-1,3],从而求得结论.解答:解:(1)∵当x∈(0,5)时,x≤f(x)≤2|x-1|+1恒成立
∴1≤f(1)≤1
∴f(1)=1;
(2)∵当x∈R时,f(x)的最小值为0,且图象关于直线x=-1对称;
∴
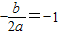 ,f(-1)=a-b+c=0
,f(-1)=a-b+c=0又∵f(1)=a+b+c=1
∴
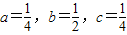
∴
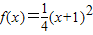 ;
;(3)设g(x)=f(x)-x=
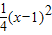
关于x=1对称
当x∈[-1,3]时,|f(x)-x|≤1
∴0≤m≤3.
点评:本题主要考查二次函数求解析式,里面有三个未知数所以要寻求三个条件来解,同时还考查了用二次函数构造新函数来研究恒成立问题,二次函数渗透性强,应用范围广,图象和性质要灵活掌握.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
设二次函数f(x)=ax2+bx+c(a>0),方程f(x)-x=0的两个根x1、x2满足0<x1<x2<
,且函数f(x)的图象关于直线x=x0对称,则有( )
| 1 |
| a |
A、x0≤
| ||
B、x0>
| ||
C、x0<
| ||
D、x0≥
|