题目内容
8．
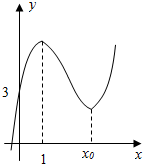已知函数f（x）=ax3+bx2+（c-3a-2b）x+d（a＞0）的图象如图．（Ⅰ）求c，d的值；
（Ⅱ）若函数f（x）在x=2处的切线方程为3x+y-11=0，求函数f（x）的解析式；
（Ⅲ）若x0=5，方程f（x）=8a有三个不同的根，求实数a的取值范围．
分析 （Ⅰ）求出函数导数，由题意可得f（0）=3，且f′（1）=0，解方程可得c，d的值；
（Ⅱ）依题意可得f′（2）=-3且f（2）=5，解方程可得a，b，进而得到f（x）的解析式；
（Ⅲ）求出导数，f′（5）=0可得b=-9a，再由图象可得方程f（x）=8a有三个不同的根，当且仅当满足f（5）＜8a＜f（1），解不等式即可得到所求范围．
解答 解：函数f（x）的导函数为f′（x）=3ax2+2bx+c-3a-2b，
（Ⅰ）由题图可知，函数f（x）的图象过点（0，3），且f′（1）=0，
得$\left\{\begin{array}{l}{d=3}\\{3a+2b+c-3a-2b=0}\end{array}\right.$解得$\left\{\begin{array}{l}{c=0}\\{d=3}\end{array}\right.$．
（Ⅱ）依题意可得f′（2）=-3且f（2）=5，得
$\left\{\begin{array}{l}{12a+4b-3a-2b=-3}\\{8a+4b-6a-4b+3=5}\end{array}\right.$，解得$\left\{\begin{array}{l}{a=1}\\{b=-6}\end{array}\right.$，
所以f（x）=x3-6x2+9x+3；
（Ⅲ）依题意f（x）=ax3+bx2+（-3a-2b）x+3（a＞0），
f′（x）=3ax2+2bx-3a-2b，
由f′（5）=75a+10b-3a-2b=0，解得b=-9a，
即有f（x）=ax3-9ax2+15ax+3，
若方程f（x）=8a有三个不同的根，当且仅当满足f（5）＜8a＜f（1），
可得3-25a＜8a＜3+7a，解得$\frac{1}{11}$＜a＜3，
所以，当得$\frac{1}{11}$＜a＜3时，方程f（x）=8a有三个不同的根．
点评 本题考查导数的运用：求切线的斜率和单调区间，考查数形结合的思想方法，考查运算能力，属于中档题．
| A． | $\frac{1}{3}$ | B． | $\frac{5}{6}$ | C． | $\frac{2}{3}$ | D． | $\frac{5}{7}$ |
若a，b是两个正整数，阅读如图的伪代码．| A． | {-1，0} | B． | {0，1} | C． | {-1，0，1} | D． | {0，1，2} |