在高200m的山顶上.测得山下一塔顶和塔底的俯角(从上往下看.视线与水平线的夹角)分别为30°.60°.则塔高为( )A．$\frac{200}{3}$mB．$\frac{200\sqrt{3}}{3}$mC．$\frac{400}{3}$mD．$\frac{400\sqrt{3}}{3}$m 题目和参考答案——青夏教育精英家教网——

题目内容

19．在高200m的山顶上，测得山下一塔顶和塔底的俯角（从上往下看，视线与水平线的夹角）分别为30°，60°，则塔高为（　　）

A．

\frac{200}{3}

$\frac{200}{3}$ m

B．

\frac{200 \sqrt{3}}{3}

$\frac{200\sqrt{3}}{3}$ m

C．

\frac{400}{3}

$\frac{400}{3}$ m

D．

\frac{400 \sqrt{3}}{3}

$\frac{400\sqrt{3}}{3}$ m

分析画出示意图，根据题意分别求得BC和BE，进而求得AE．

解答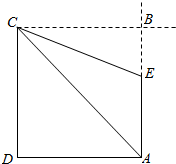解：如图，依题意知AE为塔的高度，∠ACB=60°，∠CEB=30°，AB=CD=200，
∴在△ACB中，BC= $\frac{\sqrt{3}}{3}$ AB= $\frac{\sqrt{3}}{3}$ •200，
在△BCE中，BE= $\frac{\sqrt{3}}{3}$ BC= $\frac{200}{3}$ ，
∴AE=200-BE= $\frac{400}{3}$ （m），
即塔的高度为 $\frac{400}{3}$ m，
故选C．

点评本题主要考查了解三角形问题的实际应用．解题的关键是把实际问题转变为解三角形问题．

练习册系列答案

亮点激活3加1大试卷系列答案

同步跟踪全程检测系列答案

通城学典课时新体验系列答案

亮点给力提优课时作业本系列答案

神农牛皮卷期末考向标系列答案

金钥匙课课通系列答案

15天巧夺100分系列答案

小学夺冠AB卷系列答案

课堂作业课时训练系列答案

名师点拨课时作业本系列答案

相关题目

\int_{0}^{1} （ e^{x} + 2 x ） d x =

$\int_0^1{（{e^x}+2x）dx=}$ （　　）

\frac{i}{1 + 2 i}

$\frac{i}{1+2i}$ （i是虚数单位）的虚部是（　　）

\frac{2}{5}

$\frac{2}{5}$

\frac{2}{5}

$\frac{2}{5}$

\frac{1}{5}

$\frac{1}{5}$

\frac{1}{5}

$\frac{1}{5}$

7．若函数y=f（x）（x∈D）同时满足以下条件：①它在定义域D上是单调递减或递增函数；②存在区间[a，b]?D使得f（x）在[a，b]上的值域也是[a，b]，我们将这样的函数称作“A类函数”．
（1）函数f（x）=-x³是不是“A类函数”？如果是，试找出[a，b]；如果不是，试说明理由；
（2）求使得函数g（x）=k+

\sqrt{x + 2}

$\sqrt{x+2}$ 是“A类函数”的常数k的取值范围．

14．设x∈（0，π），则函数f（x）=sinx+

\frac{4}{s i n x}

$\frac{4}{sinx}$ 的最小值是（　　）

4．已知命题p：对任意实数x都有x²+ax+a＞0恒成立；
命题q：关于x的方程x²-x+a=0有实数根；
如果“p或q”为真命题，“p且q”为假命题，求实数a的取值范围．

11．数列{a_n}的首项为a₁=1，数列{b_n}为等比数列且

b_{n} = \frac{a_{n + 1}}{a_{n}}

${b}_{n}=\frac{{a}_{n+1}}{{a}_{n}}$ ，若

{b}_{10}{b}_{11}=\root{5}{2}

${b}_{10}{b}_{11}=\root{5}{2}$ 则a₂₁=4．

8．一个角的度数是45°，化为弧度数是（　　）

\frac{π}{2}

$\frac{π}{2}$

\frac{π}{3}

$\frac{π}{3}$

\frac{π}{4}

$\frac{π}{4}$

\frac{3 i - 1}{i}

$\frac{3i-1}{i}$ 的虚部和模依次是（　　）

\sqrt{2}

$\sqrt{2}$

\sqrt{10}

$\sqrt{10}$

\sqrt{10}

$\sqrt{10}$

\sqrt{2}

$\sqrt{2}$