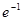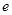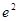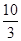题目内容
已知函数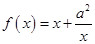 ,
,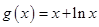 ,其中
,其中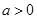 .
.
(1)若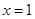 是函数
是函数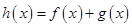 的极值点,求实数
的极值点,求实数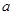 的值;
的值;
(2)若对任意的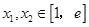 (
(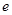 为自然对数的底数)都有
为自然对数的底数)都有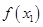 ≥
≥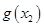 成立,求实数
成立,求实数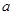 的取值范围.
的取值范围.
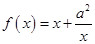 ,
,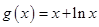 ,其中
,其中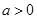 .
.(1)若
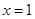 是函数
是函数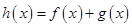 的极值点,求实数
的极值点,求实数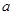 的值;
的值;(2)若对任意的
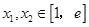 (
(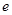 为自然对数的底数)都有
为自然对数的底数)都有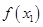 ≥
≥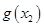 成立,求实数
成立,求实数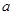 的取值范围.
的取值范围.(1)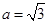 (2)
(2)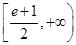
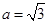 (2)
(2)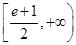
试题分析:(1)先求导,根据题意
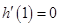 (2)可将问题转化为
(2)可将问题转化为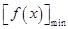 ≥
≥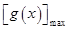 ,分别求导令导数大于0、小于0得单调性,用单调性求最值。在解导数大于0或小于0的过程中注意对
,分别求导令导数大于0、小于0得单调性,用单调性求最值。在解导数大于0或小于0的过程中注意对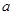 的讨论。
的讨论。试题解析:(1)解法1:∵
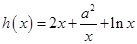 ,其定义域为
,其定义域为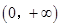 ,
,∴
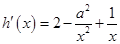 . ∵
. ∵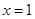 是函数
是函数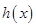 的极值点,∴
的极值点,∴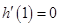 ,即
,即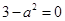 .
.∵
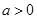 ,∴
,∴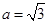 . 经检验当
. 经检验当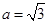 时,
时,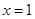 是函数
是函数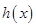 的极值点,∴
的极值点,∴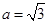 .、
.、解法2:∵
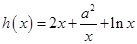 ,其定义域为
,其定义域为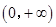 ,
,∴
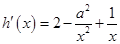 . 令
. 令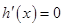 ,即
,即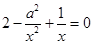 ,整理,得
,整理,得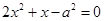 .
.∵
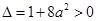 ,
,∴
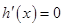 的两个实根
的两个实根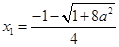 (舍去),
(舍去),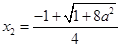 ,
,当
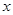 变化时,
变化时,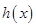 ,
,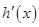 的变化情况如下表:
的变化情况如下表: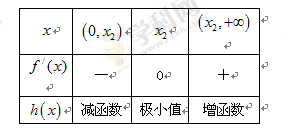
依题意,
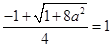 ,即
,即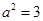 ,∵
,∵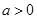 ,∴
,∴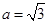 .
. (2)对任意的
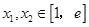 都有
都有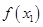 ≥
≥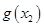 成立等价于对任意的
成立等价于对任意的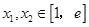 都有
都有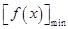 ≥
≥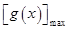 .当
.当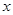
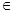 [1,
[1,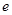 ]时,
]时,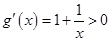 .
.∴函数
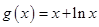 在
在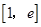 上是增函数.∴
上是增函数.∴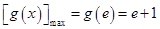 .
.∵
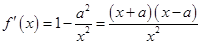 ,且
,且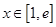 ,
,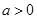 .
.①当
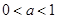 且
且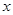
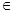 [1,
[1,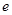 ]时,
]时,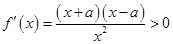 ,
,∴函数
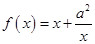 在[1,
在[1,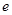 ]上是增函数,
]上是增函数,∴
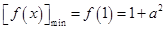 .由
.由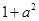 ≥
≥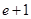 ,得
,得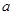 ≥
≥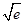 ,又
,又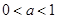 ,∴
,∴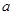 不合题意.
不合题意.②当1≤
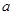 ≤
≤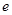 时,
时,若1≤
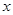 <
<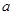 ,则
,则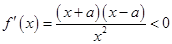 ,若
,若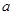 <
<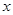 ≤
≤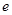 ,则
,则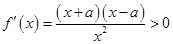 .
.∴函数
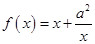 在
在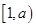 上是减函数,在
上是减函数,在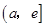 上是增函数.
上是增函数.∴
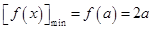 .
.由
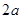 ≥
≥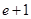 ,得
,得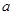 ≥
≥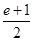 ,又1≤
,又1≤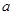 ≤
≤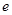 ,∴
,∴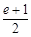 ≤
≤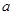 ≤
≤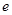 .
.③当
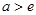 且
且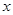
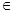 [1,
[1,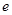 ]时,
]时,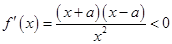 ,
,∴函数
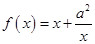 在
在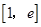 上是减函数.
上是减函数.∴
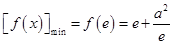 .由
.由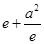 ≥
≥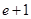 ,得
,得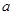 ≥
≥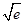 ,
,又
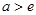 ,∴
,∴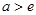 .
.综上所述,
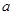 的取值范围为
的取值范围为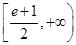 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,1)
,1)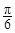 是函数
是函数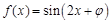 的一个零点,则函数
的一个零点,则函数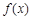 在区间
在区间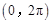 内所有极值点之和为
内所有极值点之和为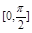 上的值域为_____________;
上的值域为_____________;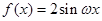
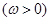 的图像在
的图像在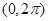 上恰有一个极大值和一个极小值,则
上恰有一个极大值和一个极小值,则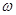 的取值范围是( )
的取值范围是( )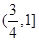
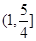
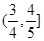
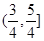
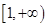 上的函数
上的函数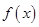 满足:①
满足:①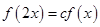 (
(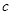 为正常数);②当
为正常数);②当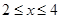 时,
时,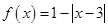 .若函数的所有极大值点均在同一条直线上,则
.若函数的所有极大值点均在同一条直线上,则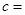 _____________.
_____________.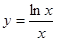 的最大值为( )
的最大值为( )