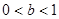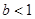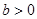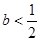题目内容
若函数f(x)=x3-3x在(a,6-a2)上有最小值,则实数a的取值范围是( )
A.(-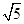 ,1) ,1) | B.[-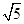 ,1) ,1) |
| C.[-2,1) | D.(-2,1) |
C
f′(x)=3x2-3=3(x+1)(x-1),令f′(x)=0,得x=±1,所以f(x)的大致图象如图所示,f(1)=-2,f(-2)=-2,若函数f(x)在(a,6-a2)上有最小值,则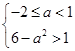 ,解得-2≤a<1.
,解得-2≤a<1.
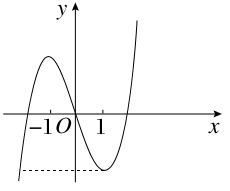
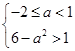 ,解得-2≤a<1.
,解得-2≤a<1.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
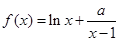 在
在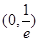 内有极值.
内有极值.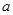 的取值范围;
的取值范围;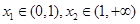 求证:
求证: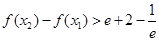 .
. 是
是 函数的两个极值点.
函数的两个极值点. 和
和 的值;
的值; 的极大值点还是极小值点,并求出相应极值.
的极大值点还是极小值点,并求出相应极值.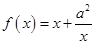 ,
,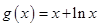 ,其中
,其中 .
. 是函数
是函数 的极值点,求实数
的极值点,求实数 的值;
的值; (
( 为自然对数的底数)都有
为自然对数的底数)都有 ≥
≥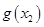 成立,求实数
成立,求实数 图象如图,则函数
图象如图,则函数




 .
. 的极大值;
的极大值; 时,存在
时,存在 图象的上方,求实数
图象的上方,求实数 的取值范围.
的取值范围.
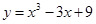 的极小值是 .
的极小值是 .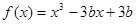 在
在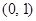 内有极小值,则
内有极小值,则