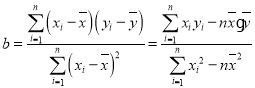题目内容
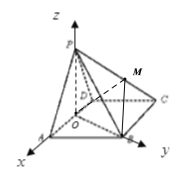
【题目】如图,在四棱锥P-ABCD中,底面ABCD为菱形且∠DAB=60°,O为AD中点.
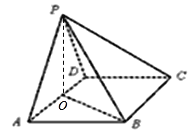
(Ⅰ)若PA=PD,求证:平面POB⊥平面PAD;
(Ⅱ)若平面PAD⊥平面ABCD,且PA=PD=AD=2,试问在线段PC上是否存在点M,使二面角M-BO-C的大小为30°,如存在,求![]() 的值,如不存在,说明理由.
的值,如不存在,说明理由.
【答案】(1)详见解析;(2)存在,![]()
【解析】
(Ⅰ)由题意可知![]() ,又
,又![]() 为菱形且
为菱形且![]() ,所以
,所以![]() ,根据线面垂直的判定定理可得
,根据线面垂直的判定定理可得![]() 平面
平面![]() ,然后再根据面面平行的判定定理可证平面
,然后再根据面面平行的判定定理可证平面![]() 平面
平面![]() ;
;
(Ⅱ)建立空间直角坐标系,利用二面角![]() 的余弦值列方程,由此求得
的余弦值列方程,由此求得![]() 的值.
的值.
(Ⅰ)因为![]() ,
,![]() 为
为![]() 中点,所以
中点,所以![]() .
.
因为四边形![]() 为菱形且
为菱形且![]() ,所以
,所以![]() .因为
.因为![]() ,所以
,所以![]() 平面
平面![]() .因为
.因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(Ⅱ)因为平面![]() 平面
平面![]() ,且交线为
,且交线为![]() ,所以
,所以![]() 平面
平面![]() .以
.以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴建立空间直角坐标系如图所示.
轴建立空间直角坐标系如图所示.
所以![]() ,
,![]() ,设
,设![]() ,所以
,所以![]() .平面
.平面![]() 的法向量为
的法向量为![]() .设平面
.设平面![]() 的法向量为
的法向量为![]() ,则
,则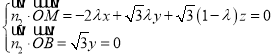 ,令
,令![]() ,则可得
,则可得![]() .
.
由于二面角![]() 的大小为
的大小为![]() ,所以
,所以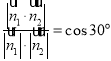 ,即
,即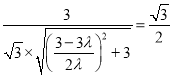 ,解得
,解得![]() .所以存在
.所以存在![]() 点使二面角
点使二面角![]() 的大小为
的大小为![]() ,且
,且![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】在统计学中,偏差是指个别测定值与测定的平均值之差,在成绩统计时,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差.某高二班主任为了了解学生的偏科情况,对学生数学偏差![]() (单位:分)与历史偏差
(单位:分)与历史偏差![]() (单位:分)之间的关系进行学科偏差分析,决定从全班52位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如下:
(单位:分)之间的关系进行学科偏差分析,决定从全班52位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如下:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学偏差 | 20 | 15 | 13 | 3 | 2 |
|
|
|
历史偏差 |
|
|
|
|
|
|
|
|
(1)已知![]() 与
与![]() 之间具有线性相关关系,求
之间具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若这次考试该班数学平均分为118分,历史平均分为![]() ,试预测数学成绩126分的同学的历史成绩.
,试预测数学成绩126分的同学的历史成绩.
附:参考公式与参考数据
 ,
,![]() ,
,![]() ,
,![]() .
.