题目内容
【题目】甲、乙两人各进行![]() 次射击,甲每次击中目标的概率为
次射击,甲每次击中目标的概率为![]() ,乙每次击中目标的概率
,乙每次击中目标的概率![]() ,
,
(Ⅰ)记甲击中目标的次数为![]() ,求
,求![]() 的概率分布及数学期望;
的概率分布及数学期望;
(Ⅱ)求甲恰好比乙多击中目标![]() 次的概率.
次的概率.
【答案】(1)分布列(见解析),Eξ=1.5;(2)![]() .
.
【解析】
试题(1)因甲每次是否击中目标相互独立,所以ξ服从二项分布,即![]() ,由期望
,由期望![]() 或
或![]() (二项分布);(2)甲恰好比乙多击中目标2次:分为2类,甲3次乙1次,甲2次乙0次.甲乙相互独立概率相乘.
(二项分布);(2)甲恰好比乙多击中目标2次:分为2类,甲3次乙1次,甲2次乙0次.甲乙相互独立概率相乘.
试题解析:
甲射击三次其集中次数ξ服从二项分布:
(1)P(ξ=0)=![]() P(ξ=1)=
P(ξ=1)=![]()
P(ξ=2)=![]() P(ξ=3)=
P(ξ=3)=![]() 4分
4分
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
ξ的概率分布如下表:
Eξ=![]() , 8分
, 8分
(2)甲恰好比乙多击中目标2次:分为2类,甲3次乙1次,甲2次乙0次.甲乙相互独立概率相乘.
![]() . 12分
. 12分

【题目】总体由编号为![]() 的20个个体组成,利用下面的随机数表选取6个个体,选取方法是从随机数表第一行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第6个个体的编号为( )
的20个个体组成,利用下面的随机数表选取6个个体,选取方法是从随机数表第一行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第6个个体的编号为( )
7816 | 6572 | 0802 | 6314 | 0702 | 4369 | 1128 | 0598 |
3204 | 9234 | 4935 | 8200 | 3623 | 4869 | 6938 | 7481 |
A.08B.07C.02D.05
【题目】为了了解某省各景点在大众中的熟知度,随机对15~65岁的人群抽样了![]() 人,回答问题“某省有哪几个著名的旅游景点?”统计结果如下图表
人,回答问题“某省有哪几个著名的旅游景点?”统计结果如下图表
组号 | 分组 | 回答正确 的人数 | 回答正确的人数 占本组的频率 |
第1组 | [15,25) |
| 0.5 |
第2组 | [25,35) | 18 |
|
第3组 | [35,45) |
| 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 |
|
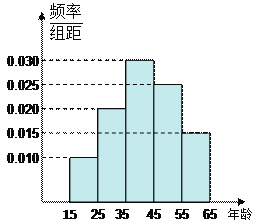
(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
(3)在(2)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.