题目内容
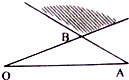 如图,点P所在的区域为线段AB,OB的延长线所形成的区域,即图中阴影部分(不含边界),若
如图,点P所在的区域为线段AB,OB的延长线所形成的区域,即图中阴影部分(不含边界),若| OP |
| OA |
| OB |
A、(1,
| ||||
B、(-
| ||||
C、(
| ||||
D、(-
|
考点:二元一次不等式(组)与平面区域,平面向量的坐标运算
专题:平面向量及应用
分析:分析:本题考查的知识点是平面向量的基本定理和平行四边形法则,可以将四个答案一一代入,判断点的位置,排除错误答案,即可得到结论.
解答:解答:解:根据平面向量基本定理和平行四边形法则,
若A(1,
),则
=
+
,此时P在阴影部分的下方,不成立.
若B(-
,
),则
=-
+
,此时P在阴影部分的下方,不成立.
若C(
,-1),则
=
-
,此时P在阴影部分的上方,成立.
若D(-
,2),则
=-
+2
,此时P在阴影部分的下方,不成立.
故选:C
若A(1,
| 1 |
| 2 |
| OP |
| OA |
| 1 |
| 2 |
| OB |
若B(-
| 2 |
| 3 |
| 5 |
| 3 |
| OP |
| 2 |
| 3 |
| OA |
| 5 |
| 3 |
| OB |
若C(
| 5 |
| 3 |
| OP |
| 5 |
| 3 |
| OA |
| OB |
若D(-
| 1 |
| 2 |
| OP |
| 1 |
| 2 |
| OA |
| OB |
故选:C
点评:本题主要考查平面向量的应用,利用向量的基本定理是解决本题的关键.

练习册系列答案
相关题目
函数f(x)=(sinx+cosx)2的一条对称轴的方程是( )
A、x=
| ||
B、x=
| ||
C、x=
| ||
| D、x=π |
等差数列{αn}中,α1=33,d=-4,若前n项和Sn取得最大,则n=( )
| A、9 | B、10 | C、11 | D、12 |
已知正项等比数列{an}满足4a1,2a2,a3成等差数列,若存在两项am,an,使得
=4a1,则
+
的最小值为( )
| aman |
| 1 |
| m |
| 9 |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
不等式
>2的解集为( )
| x-1 |
| x |
| A、{x|x<-1或x>0} |
| B、{x|x<-1} |
| C、{x|x>-1} |
| D、{x|-1<x<0} |
给出下列四个命题:命题p1:?a,b∈(0,+∞),当a+b=1时,
+
=
;命题p2:函数y=ln
是奇函数,则下列命题是真命题的是( )
| 1 |
| a |
| 1 |
| b |
| 7 |
| 2 |
| 1-x |
| 1+x |
| A、p1∨p2 |
| B、p1∨¬p2 |
| C、p1∧p2 |
| D、p1∧¬p2 |
已知椭圆C:
+
=1的左、右焦点分别为F1,F2,P为椭圆C上一点,若△F1F2P为等腰直角三角形,则椭圆C的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,某搬运工人将一长为
如图,某搬运工人将一长为