题目内容
函数f（x）=（sinx+cosx）2的一条对称轴的方程是（ ）
A、x=
| ||
B、x=
| ||
C、x=
| ||
| D、x=π |
考点：三角函数中的恒等变换应用,正弦函数的图象
专题：计算题,三角函数的图像与性质
分析：利用三角函数中的平方关系与二倍角的正弦，可知f（x）=1+sin2x，利用其对称性可求得其对称轴方程，从而可从选项A、B、C、D中得到答案．
解答：解：∵f（x）=（sinx+cosx）2
=sin2x+2sinxcosx+cos2x
=1+sin2x，
由2x=kπ+
（k∈Z）得：x=
+
（k∈Z），
令k=0得，x=
，
∴函数f（x）=（sinx+cosx）2的一条对称轴的方程x=
，
故选：A．
=sin2x+2sinxcosx+cos2x
=1+sin2x，
由2x=kπ+
| π |
| 2 |
| kπ |
| 2 |
| π |
| 4 |
令k=0得，x=
| π |
| 4 |
∴函数f（x）=（sinx+cosx）2的一条对称轴的方程x=
| π |
| 4 |
故选：A．
点评：本题考查三角函数中的恒等变换应用，着重考查正弦函数的对称性，属于中档题．
练习册系列答案
53随堂测系列答案
相关题目
如图是一个根据△ABC的三条边的边长a，b，c判断三角形形状的程序框图，则框图中菱形内应该填写的是（ ）| A、a＞c？ | B、a＜c？ | C、b＞c？ | D、b＜c？ |
函数f（x）=cosx在区间[a，b]上是增函数，且f（a）=-1，f（b）=1，则sin
=（ ）
| a+b |
| 4 |
A、±
| ||||
B、
| ||||
| C、±1 | ||||
D、-
|
已知向量
=（1，2），
=（1，0），
=（3，4），若λ为实数，（
+λ
）⊥
，则λ的值为（ ）
| a |
| b |
| c |
| b |
| a |
| c |
A、
| ||
B、-
| ||
| C、1 | ||
D、-
|
如图，四边形ABCD是半径为1的圆O的外切正方形，△PQR是圆O的内接正三角形，当△PQR绕着圆心O旋转时，| AQ |
| OR |
A、[1-
| ||||||||
B、[-1-
| ||||||||
C、[-
| ||||||||
D、[
|
已知△ABC的外心P满足
=
（
+
），cosA=（ ）
| AP |
| 1 |
| 3 |
| AB |
| AC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若m≠n，两个等差数列m，a1，a2，n与m，b1，b2，b3，n的公差分别为d1和d2，则
的值为（ ）
| d2 |
| d1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
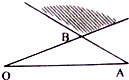如图，点P所在的区域为线段AB，OB的延长线所形成的区域，即图中阴影部分（不含边界），若| OP |
| OA |
| OB |
A、（1，
| ||||
B、（-
| ||||
C、（
| ||||
D、（-
|
下列命题中真命题是（ ）
| A、相关系数r（|r|≤1），|r|值越小，变量之间的线性相关程度越高 | B、“存在x∈R，使得x2+x+1＜0”的否定是“对任意x∈R．均有x2+x+1＜0” | C、命题“在△ABC中，若A＞B，则sinA＞sinB”的逆命题为假命题 | D、“b=0”是“函数f（x）=ax2+bx+c是偶函数”的充要条件 |