题目内容
已知椭圆C:
+
=1的左、右焦点分别为F1,F2,P为椭圆C上一点,若△F1F2P为等腰直角三角形,则椭圆C的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:求椭圆的离心率,即求参数a,c的关系,本题中给出了三角形PF1F2为等腰三角形这一条件,由相关图形知,角P或F1或角F2为直角,不妨令角F2为直角,
则有PF2=F1F2,求出两线段的长度,代入此方程,整理即可得到所求的离心率.
则有PF2=F1F2,求出两线段的长度,代入此方程,整理即可得到所求的离心率.
解答:由题意,角P或F1或角F2为直角,
当P为直角时,b=c,
∴a2=b2+c2=2c2
∴离心率e=
=
;
当角F1或角F2为直角,
不妨令角F2为直角,
此时P(c,y),代入椭圆方程
+
=1得y=±
,
又三角形PF1F2为等腰三角形得PF2=F1F2,
故得PF2═2c,即a2-c2=2ac,
解得
=
-1,
即椭圆C的离心率为
-1.
故选C.
当P为直角时,b=c,
∴a2=b2+c2=2c2
∴离心率e=
| c |
| a |
| ||
| 2 |
当角F1或角F2为直角,
不妨令角F2为直角,
此时P(c,y),代入椭圆方程
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
又三角形PF1F2为等腰三角形得PF2=F1F2,
故得PF2═2c,即a2-c2=2ac,
解得
| c |
| a |
| 2 |
即椭圆C的离心率为
| 2 |
故选C.
点评:本题考查椭圆的性质和应用,解题时要注意公式的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
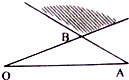 如图,点P所在的区域为线段AB,OB的延长线所形成的区域,即图中阴影部分(不含边界),若
如图,点P所在的区域为线段AB,OB的延长线所形成的区域,即图中阴影部分(不含边界),若| OP |
| OA |
| OB |
A、(1,
| ||||
B、(-
| ||||
C、(
| ||||
D、(-
|
下列命题中真命题是( )
| A、相关系数r(|r|≤1),|r|值越小,变量之间的线性相关程度越高 | B、“存在x∈R,使得x2+x+1<0”的否定是“对任意x∈R.均有x2+x+1<0” | C、命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题 | D、“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件 |
sinα=sinβ是α=β的( )
| A、充分不必要条件 | B、必要不充分条件 | C、充要条件 | D、既不充分又不必要条件 |
“a≤0”是函数f(x)=|x(2-ax)|在区间(0,+∞)内单调递增”的( )
| A、充分不必要条件 | B、必要不充分条件 | C、充分必要条件 | D、既不充分也不必要条件 |
已知双曲线
-
=1(a>0,b>0)的一条渐近线方程是y=
x,它的一个焦点在抛物线y2=48x的准线上,则双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知直线y=k(x+1)与抛物线C:y2=4x相交于点A,B两点,F为抛物线C的焦点,若|FA|=3|FB|,则k=( )
A、±
| ||||
B、±
| ||||
C、±
| ||||
D、±
|
函数f(x)=-x3+3x2-4的单调递增区间是( )
| A、(-∞,0) | B、(-2,0) | C、(0,2) | D、(2,+∞) |
复数
(i为虚数单位)在复平面上对应的点在( )
| 2+i |
| i3 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |