题目内容
给出下列四个命题:命题p1:?a,b∈(0,+∞),当a+b=1时,
+
=
;命题p2:函数y=ln
是奇函数,则下列命题是真命题的是( )
| 1 |
| a |
| 1 |
| b |
| 7 |
| 2 |
| 1-x |
| 1+x |
| A、p1∨p2 |
| B、p1∨¬p2 |
| C、p1∧p2 |
| D、p1∧¬p2 |
考点:复合命题的真假
专题:简易逻辑
分析:首先对两个命题一一加以判断,对第一个命题注意运用基本不等式,求出最小值4,即可判断;对第二个运用函数的奇偶性的定义即可判断,再根据复合命题的真假及真值表加以判断四个选项.
解答:解:对命题P1,由于a,b>0,当a+b=1时,
+
=
+
=2+
+
≥2+2
=4,当且仅当a=b=
时,取得最小值为4,故P1为假命题;
对命题P2,函数y=ln
的定义域为(-1,1),f(-x)+f(x)=ln
+ln
=ln1=0,故函数为奇函数,即P2为真命题,
故A.P1∨P2为真,B.P1∨¬P2为假,C.P1∧P2为假,D.P1∧¬P2为假.
故选A.
| 1 |
| a |
| 1 |
| b |
| a+b |
| a |
| a+b |
| b |
| a |
| b |
| b |
| a |
|
| 1 |
| 2 |
对命题P2,函数y=ln
| 1-x |
| 1+x |
| 1+x |
| 1-x |
| 1-x |
| 1+x |
故A.P1∨P2为真,B.P1∨¬P2为假,C.P1∧P2为假,D.P1∧¬P2为假.
故选A.
点评:本题主要考查复合命题的真假判断,注意运用真值表,同时考查基本不等式的运用和函数的奇偶性的定义,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=cosx在区间[a,b]上是增函数,且f(a)=-1,f(b)=1,则sin
=( )
| a+b |
| 4 |
A、±
| ||||
B、
| ||||
| C、±1 | ||||
D、-
|
若m≠n,两个等差数列m,a1,a2,n与m,b1,b2,b3,n的公差分别为d1和d2,则
的值为( )
| d2 |
| d1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
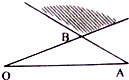 如图,点P所在的区域为线段AB,OB的延长线所形成的区域,即图中阴影部分(不含边界),若
如图,点P所在的区域为线段AB,OB的延长线所形成的区域,即图中阴影部分(不含边界),若| OP |
| OA |
| OB |
A、(1,
| ||||
B、(-
| ||||
C、(
| ||||
D、(-
|
如果关于x的不等式
>0的解集为(-1,3),则不等式
<0的解集是( )
| ax-1 |
| x+b |
| 2ax+1 |
| 2x-b |
A、(-∞,-
| ||||
B、(-
| ||||
C、(-∞,-
| ||||
D、(-
|
已知命题p:?α∈R,sin(π-α)=cosα;命题q:m>0是双曲线
-
=1的离心率为
的充分不必要条件.则下面结论正确的是( )
| x2 |
| m2 |
| y2 |
| m2 |
| 2 |
| A、p∧(¬q)是真命题 |
| B、(¬p)∨q是真命题 |
| C、p∧q是假命题 |
| D、p∨q是假命题 |
下列命题中真命题是( )
| A、相关系数r(|r|≤1),|r|值越小,变量之间的线性相关程度越高 | B、“存在x∈R,使得x2+x+1<0”的否定是“对任意x∈R.均有x2+x+1<0” | C、命题“在△ABC中,若A>B,则sinA>sinB”的逆命题为假命题 | D、“b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件 |
已知直线y=k(x+1)与抛物线C:y2=4x相交于点A,B两点,F为抛物线C的焦点,若|FA|=3|FB|,则k=( )
A、±
| ||||
B、±
| ||||
C、±
| ||||
D、±
|