题目内容
如图，某搬运工人将一长为| 3 |
考点：弧度制
专题：解三角形
分析：根据弧长公式，求得l=lAA1+lA1A2+lA2A3，再根据扇形的面积公式，求得S=S1+S2+S3，问题得以解决．
解答：解：l=lAA1+lA1A2+lA2A3=
×2+
×1+
×
=
π．
S=S1+S2+S3=
（l1R1+l2R2+l3R3）=
（2π+
×1+
×
）=2π．
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 3 |
3+
| ||
| 2 |
S=S1+S2+S3=
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| ||
| 2 |
| 3 |
点评：本题主要考查了弧长公式和扇形的面积公式，属于基础题．
练习册系列答案
相关题目
在空间直角坐标系中，若P（3，-2，1）则P点关于坐标平面xOz的对称点坐标为（ ）
| A、（-3，-2，-1） | B、（3，2，1） | C、（-3，2，-1） | D、（3，-2，-1） |
如图是一个根据△ABC的三条边的边长a，b，c判断三角形形状的程序框图，则框图中菱形内应该填写的是（ ）| A、a＞c？ | B、a＜c？ | C、b＞c？ | D、b＜c？ |
将区间[0，1]内的随机数转化为[-2，6]内的均匀随机数，需实施的变换为（ ）
| A、a=a1*8 | B、a=a1*8+2 | C、a=a1*8-2 | D、a=a1*6 |
如图，矩形OABC的阴影部分是由曲线f（x）=sinx，直线x=| 2π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设角α的终边与单位圆相交于点P（
，-
），则sinα-cosα的值是（ ）
| 3 |
| 5 |
| 4 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
函数f（x）=cosx在区间[a，b]上是增函数，且f（a）=-1，f（b）=1，则sin
=（ ）
| a+b |
| 4 |
A、±
| ||||
B、
| ||||
| C、±1 | ||||
D、-
|
已知向量
=（1，2），
=（1，0），
=（3，4），若λ为实数，（
+λ
）⊥
，则λ的值为（ ）
| a |
| b |
| c |
| b |
| a |
| c |
A、
| ||
B、-
| ||
| C、1 | ||
D、-
|
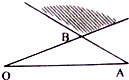如图，点P所在的区域为线段AB，OB的延长线所形成的区域，即图中阴影部分（不含边界），若| OP |
| OA |
| OB |
A、（1，
| ||||
B、（-
| ||||
C、（
| ||||
D、（-
|