题目内容
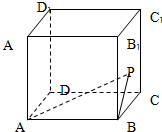
如图,正方体ABCD-A1B1C1D1棱长为1,P为侧面BB1C1C内的动点,且PA=2PB,则P点所形成轨迹图形的长度为( )
A.
| B.
| C.π | D.
|

以点D为坐标原点,DA为x轴,DC为y轴,DD′为z轴建立空间直角坐标系,则A(1,0,0),B(1,1,0),
∵P为侧面BB1C1C内的动点,故点P的纵坐标为1,
设P(x,1,z),
则|PA|=
,|PB|=
,
∵PA=2PB,
∴(
)2=4(
)2,
∴(x-1)2+z2=
,
∴点P是以(1,1,0)为圆心,以
为半径的球与面BB1C1C内相交的圆面.
∴轨迹图形的长度为该圆的周长2π×
=
π.
故选B.
∵P为侧面BB1C1C内的动点,故点P的纵坐标为1,
设P(x,1,z),
则|PA|=
| (x-1)2+(1-0)2+z2 |
| (x-1)2+(1-1)2+z2 |
∵PA=2PB,
∴(
| (x-1)2+(1-0)2+z2 |
| (x-1)2+(1-1)2+z2 |
∴(x-1)2+z2=
| 1 |
| 3 |
∴点P是以(1,1,0)为圆心,以
| ||
| 3 |
∴轨迹图形的长度为该圆的周长2π×
| ||
| 3 |
2
| ||
| 3 |
故选B.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
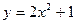 上运动,定点A(0,-1),若点M分
上运动,定点A(0,-1),若点M分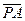 所成的比为2,则动点M的轨迹方程是 .
所成的比为2,则动点M的轨迹方程是 .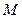 为抛物线
为抛物线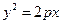
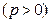 上任一点,
上任一点,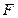 为焦点,则以
为焦点,则以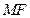 为直径的圆与
为直径的圆与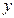 轴的位置关系是 。
轴的位置关系是 。
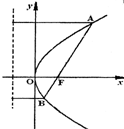
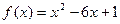 的对称轴方程是 .
的对称轴方程是 .