题目内容
【题目】已知函数![]() 对任意实数x、y恒有
对任意实数x、y恒有![]() ,当x>0时,f(x)<0,且
,当x>0时,f(x)<0,且![]() .
.
(1)判断![]() 的奇偶性;
的奇偶性;
(2)求![]() 在区间[-3,3]上的最大值;
在区间[-3,3]上的最大值;
(3)若![]() 对所有的
对所有的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)奇函数(2)6(3)![]() 或者
或者![]()
【解析】
(1)令x=y=0f(0)=0,再令y=﹣x,f(﹣x)=﹣f(x);
(2)设x1,x2∈R,且x1<x2,结合条件用单调性的定义证明函数f(x)为R上的增函数,从而得到![]() 在区间[-3,3]上的最大值;
在区间[-3,3]上的最大值;
(3)根据函数f(x)≤m2﹣2am﹣2对所有的x∈[﹣1,1],a∈[﹣1,1]恒成立,说明f(x)的最大值2小于右边,因此先将右边看作a的函数,m为参数系数,解不等式组,即可得出m的取值范围.
(1)取x=y=0,则f(0+0)=f(0)+f(0);则f(0)=0;
取y=﹣x,则f(x﹣x)=f(x)+f(﹣x),
∴f(﹣x)=﹣f(x)对任意x∈R恒成立
∴f(x)为奇函数;
(2)任取x1,x2∈(﹣∞,+∞)且x1<x2,则x2﹣x1>0;∴f(x2)+f(﹣x1)=f(x2﹣x1)<0;
∴f(x2)<﹣f(﹣x1),
又∵f(x)为奇函数,
∴f(x1)>f(x2);
∴f(x)在(﹣∞,+∞)上是减函数;
∴对任意x∈[﹣3,3],恒有f(x)≤f(﹣3)
而f(3)=f(2+1)=f(2)+f(1)=3f(1)=﹣2×3=﹣6;
∴f(﹣3)=﹣f(3)=6;
∴f(x)在[﹣3,3]上的最大值为6;
(3)由(2)可知函数![]() 在
在![]() 的最大值为
的最大值为![]()
所以要使![]() 对所有的
对所有的![]() 恒成立
恒成立
只需要![]()
即![]() 对所有
对所有![]() 恒成立
恒成立
令![]() ,则
,则![]() 即
即![]() 解得
解得![]()
所以实数![]() 的取值范围是
的取值范围是![]()

 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案【题目】一只红铃虫的产卵数y和温度x有关,现收集了6组观测数据于下表中,通过散点图可以看出样本点分布在一条指数型函数y=![]() 的图象的周围.
的图象的周围.
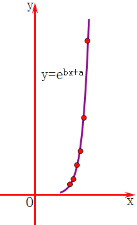
(1)试求出y关于x的上述指数型的回归曲线方程(结果保留两位小数);
(2)试用(1)中的回归曲线方程求相应于点(24,17)的残差![]() .(结果保留两位小数)
.(结果保留两位小数)
温度x(°C) | 20 | 22 | 24 | 26 | 28 | 30 |
产卵数y(个) | 6 | 9 | 17 | 25 | 44 | 88 |
z=lny | 1.79 | 2.20 | 2.83 | 3.22 | 3.78 | 4.48 |
几点说明:
①结果中的![]() 都应按题目要求保留两位小数.但在求
都应按题目要求保留两位小数.但在求![]() 时请将
时请将![]() 的值多保留一位即用保留三位小数的结果代入.
的值多保留一位即用保留三位小数的结果代入.
②计算过程中可能会用到下面的公式:回归直线方程的斜率![]() =
=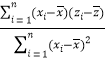 =
=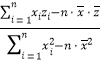 ,截距
,截距![]() .
.
③下面的参考数据可以直接引用:![]() =25,
=25,![]() =31.5,
=31.5,![]() ≈3.05,
≈3.05,![]() =5248,
=5248,![]() ≈476.08,
≈476.08,![]() ,ln18.17≈2.90.
,ln18.17≈2.90.
【题目】某校倡导为特困学生募捐,要求在自动购水机处每购买一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出矿泉水箱数和收入情况,列表如下:
售出水量 | 7 | 6 | 6 | 5 | 6 |
收入 | 165 | 142 | 148 | 125 | 150 |
学校计划将捐款以奖学金的形式奖励给品学兼优的特困生,规定:特困生综合考核前20名,获一等奖学金500元;综合考核21-50名,获二等奖学金300元;综合考核50名以后的不获得奖学金.
(1)若![]() 与
与![]() 成线性相关,则某天售出9箱水时,预计收入为多少元?
成线性相关,则某天售出9箱水时,预计收入为多少元?
(2)假设甲、乙、丙三名学生均获奖,且各自获一等奖和二等奖的可能性相同,求三人获得奖学金之和不超过1000元的概率.
附:回归方程![]() ,其中
,其中 .
.