Question

【题目】已知函数是定义域在上的奇函数，且．

（1）用定义证明：函数在上是增函数，

（2）若实数满足，求实数的范围．

Answer 1

【答案】（1）证明见解析（2）

【解析】

（1）根据求得，根据单调性的定义，计算，由此证得函数在上为增函数.

（2）利用函数的奇偶性化简，再利用函数的单调性结合函数的定义域列不等式组，解不等式组求得的取值范围.

（1）∵函数是定义域为（-1，1）上的奇函数，

∴f（0）=0，∴b=0，

∴

任取x1，x2∈（-1，1），且x1＜x2，

∴f（x1）-f（x2）=-

==，

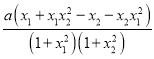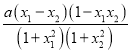∵a＞0，-1＜x1＜x2＜1，

∴x1-x2＜0，1-x1x2＞0，1+＞0，1+＞0，

∴函数f（x）在（-1，1）上是增函数．

（2）∵f（2t-1）+f（t-1）＜0，∴f（2t-1）＜-f（t-1），

∵函数是定义域为（-1，1）上的奇函数，且a＞0．

∴f（2t-1）＜f（1-t），

∵函数f（x）在（-1，1）上是增函数，

∴，

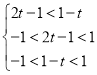解得．

故实数t的范围是．