题目内容
16.观察①sin210°+cos240°+sin10°cos40°=$\frac{3}{4}$;②sin26°+cos236°+sin6°cos36°=$\frac{3}{4}$;③sin215°+cos245°+sin15°cos45°=$\frac{3}{4}$,猜想一个一般的式子,并证明.分析 观察所给的等式,写出结果sin2α+cos2(30°+α)+sinαcos(30°+α)=$\frac{3}{4}$,再进行证明即可.
解答 解:sin2α+cos2(30°+α)+sinαcos(30°+α)=$\frac{3}{4}$.
可以证明此结论是正确的,证明如下:
sin2α+cos2(30°+α)+sinα•cos(30°+α)
=$\frac{1-cos2α}{2}$+$\frac{1+cos(60°+2α)}{2}$+$\frac{1}{2}$[sin(30°+2α)-sin30°]
=1+$\frac{1}{2}$[cos(60°+2α)-cos2α]+$\frac{1}{2}$sin(30°+2α)-$\frac{1}{2}$
=1+$\frac{1}{2}$[-2sin(30°+2α)sin30°]+$\frac{1}{2}$sin(30°+2α)-$\frac{1}{2}$
=$\frac{3}{4}$-$\frac{1}{2}$sin(30°+2α)+$\frac{1}{2}$sin(30°+2α)=$\frac{3}{4}$.
点评 本题考查类比推理,考查对于所给的式子的理解,从所给式子出发,通过观察、类比、猜想出一般规律,不需要证明结论,该题着重考查了类比的能力.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
7.如图所示的程序框图,输出的S的值为( )
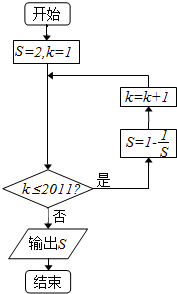

| A. | $\frac{1}{2}$ | B. | 2 | C. | -1 | D. | -$\frac{1}{2}$ |
1.演绎推理“因为指数函数y=ax(a>0,a≠1)是增函数,而函数y=0.5x是指数函数,所以y=0.5x是增函数”,所得结论错误的原因是( )
| A. | 大前提错误 | B. | 小前提错误 | ||
| C. | 推理形式错误 | D. | 大前提与小前提均错误 |
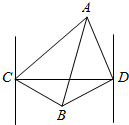 如图,一轮船自西向东匀速行驶,在C处测得A岛在东北方向,B岛在南偏东60°方向,此船向东航行6000海里后到达D处,测得A岛在北偏西15°方向,B岛在南偏西75°方向,则A,B两岛间距离为1000$\sqrt{42}$海里(结果保留根号).
如图,一轮船自西向东匀速行驶,在C处测得A岛在东北方向,B岛在南偏东60°方向,此船向东航行6000海里后到达D处,测得A岛在北偏西15°方向,B岛在南偏西75°方向,则A,B两岛间距离为1000$\sqrt{42}$海里(结果保留根号).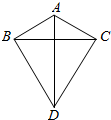 如图,在△ABC中,AB=AC=a,以BC为边向外作正三角形BCD,则AD的最大值为2a.
如图,在△ABC中,AB=AC=a,以BC为边向外作正三角形BCD,则AD的最大值为2a. 如图,该程序框图的算法思路源于我国古代数学专著《九章算术》中的“更相减损术”,执行此程序框图,若输入的m,n分别为72,168,则输出的m=( )
如图,该程序框图的算法思路源于我国古代数学专著《九章算术》中的“更相减损术”,执行此程序框图,若输入的m,n分别为72,168,则输出的m=( )