题目内容
8.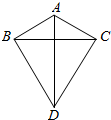 如图,在△ABC中,AB=AC=a,以BC为边向外作正三角形BCD,则AD的最大值为2a.
如图,在△ABC中,AB=AC=a,以BC为边向外作正三角形BCD,则AD的最大值为2a.
分析 如图所示,设BC=2x,由于△BCD是等边三角形,可得DE=$\sqrt{3}$x,在Rt△ABE中,AE=$\sqrt{{a}^{2}-{x}^{2}}$,AD=$\sqrt{{a}^{2}-{x}^{2}}$+$\sqrt{3}$x,设x=acosθ,$θ∈(0,\frac{π}{2})$,利用和差公式可得:AD=2a$sin(θ+\frac{π}{3})$,利用三角函数的单调性即可得出.
解答 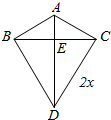 解:如图所示,
解:如图所示,
设BC=2x,
∵△BCD是等边三角形,∴DE=$\sqrt{3}$x,
在Rt△ABE中,AE=$\sqrt{{a}^{2}-{x}^{2}}$,
则AD=$\sqrt{{a}^{2}-{x}^{2}}$+$\sqrt{3}$x,
设x=acosθ,$θ∈(0,\frac{π}{2})$,
则AD=asinθ+$\sqrt{3}acosθ$
=2a$sin(θ+\frac{π}{3})$,
∵$(θ+\frac{π}{3})$∈$(\frac{π}{3},\frac{5π}{6})$.
∴$sin(θ+\frac{π}{3})$≤1,
∴AD≤2a,
因此AD的最大值为 2a.
故答案为:2a.
点评 本题考查了等边三角形的性质、三角函数的单调性、和差公式、三角形三边大小关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18. 如图所示是一个有n层(n≥2,n∈N*)的六边形点阵,它的中心是一个点,算作第1层,第2层每边有2个点,第3层每边有3个点,…,第n层每边有n个点,则这个点阵共有( )个点.
如图所示是一个有n层(n≥2,n∈N*)的六边形点阵,它的中心是一个点,算作第1层,第2层每边有2个点,第3层每边有3个点,…,第n层每边有n个点,则这个点阵共有( )个点.
 如图所示是一个有n层(n≥2,n∈N*)的六边形点阵,它的中心是一个点,算作第1层,第2层每边有2个点,第3层每边有3个点,…,第n层每边有n个点,则这个点阵共有( )个点.
如图所示是一个有n层(n≥2,n∈N*)的六边形点阵,它的中心是一个点,算作第1层,第2层每边有2个点,第3层每边有3个点,…,第n层每边有n个点,则这个点阵共有( )个点.| A. | n2 | B. | n2+n | C. | 3n2-3n+1 | D. | 3n2-3n |
19.若输出k的值为6,则判断框内可填入的条件是( )
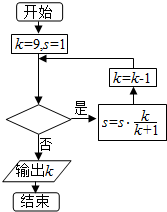

| A. | s>$\frac{1}{2}$ | B. | s>$\frac{3}{5}$ | C. | s>$\frac{7}{10}$ | D. | s>$\frac{4}{5}$ |
3.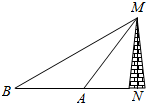 如图,要测量电视塔的高度,测量者在点A处测得对电视塔的仰角为60°,然后测量者后退200米到点B,测得对电视塔的仰角为30°,则电视塔的高度为( )
如图,要测量电视塔的高度,测量者在点A处测得对电视塔的仰角为60°,然后测量者后退200米到点B,测得对电视塔的仰角为30°,则电视塔的高度为( )
 如图,要测量电视塔的高度,测量者在点A处测得对电视塔的仰角为60°,然后测量者后退200米到点B,测得对电视塔的仰角为30°,则电视塔的高度为( )
如图,要测量电视塔的高度,测量者在点A处测得对电视塔的仰角为60°,然后测量者后退200米到点B,测得对电视塔的仰角为30°,则电视塔的高度为( )| A. | 100$\sqrt{2}$m | B. | 100$\sqrt{3}$m | C. | 100m | D. | 200m |
17.设有一个边长为3的正三角形,记为A1,将A1的每边三等分,在中间的线段上向形外作正三角形,去掉中间的线段后得到的图形记为A2,将A2的每边三等分,再重复上述过程,得到图象A3,再重复上述过程,得到图形A4,A5,则A3的周长是( )
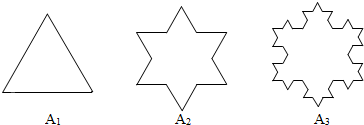

| A. | 16 | B. | $\frac{16}{3}$ | C. | $\frac{256}{9}$ | D. | $\frac{128}{3}$ |
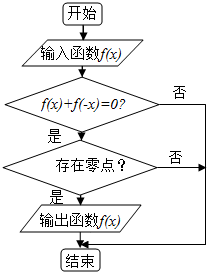 某程序框图如图所示,现输入如下四个函数,其中可以输出的函数是f(x)=sinx.
某程序框图如图所示,现输入如下四个函数,其中可以输出的函数是f(x)=sinx.