题目内容
4.二维空间中圆的一维测度(周长)l=2πr,二维测度(面积)S=πr2,则S′=l;三维空间中球的二维测度(表面积)S=4πr2,三维测度(体积)V=$\frac{4}{3}$πr3,则V′=S.已知四维空间中“超球”的三维测度V=8πr3,猜想其四维测度W=2πr4.分析 根据所给的示例及类比推理的规则得出高维的测度的导数是底一维的测度,从而得到W′=V,从而求出所求.
解答 解:∵二维空间中圆的一维测度(周长)l=2πr,二维测度(面积)S=πr2,观察发现S′=l
三维空间中球的二维测度(表面积)S=4πr2,三维测度(体积)V=$\frac{4}{3}$πr3,观察发现V′=S
∴四维空间中“超球”的三维测度V=8πr3,猜想其四维测度W,则W′=V=8πr3;
∴W=2πr4.
故答案为:2πr4
点评 本题考查类比推理,解题的关键是理解类比的规律,解题的关键主要是通过所给的示例及类比推理的规则得出高维的测度的导数是低一维的测度,属于基础题.

练习册系列答案
相关题目
4.1.2log6$\sqrt{2}$+3log6$\root{3}{3}$=( )
| A. | 0 | B. | 1 | C. | 6 | D. | log6$\frac{2}{3}$ |
15.双曲线$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1的焦点坐标为( )
| A. | (±$\sqrt{7}$,0) | B. | (0,±$\sqrt{7}$) | C. | (±5,0) | D. | (0,±5) |
19.若输出k的值为6,则判断框内可填入的条件是( )
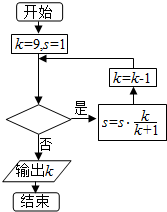

| A. | s>$\frac{1}{2}$ | B. | s>$\frac{3}{5}$ | C. | s>$\frac{7}{10}$ | D. | s>$\frac{4}{5}$ |
9.阅读程序框图,如果输出i=5,那么在空白矩形框中填入的语句为( )
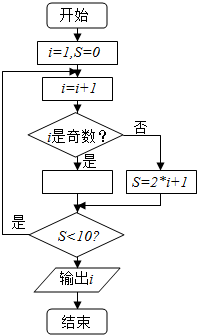

| A. | S=2*i+4 | B. | S=2*i-1 | C. | S=2*i-2 | D. | S=2*i |
14.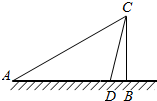 如图,某人欲测量某建筑物的高度BC,在A处测得建筑物顶端C的仰角为30°,然后,向建筑物方向前进200m到达D处,在D处测得C的仰角为75°,则建筑物的高度为( )
如图,某人欲测量某建筑物的高度BC,在A处测得建筑物顶端C的仰角为30°,然后,向建筑物方向前进200m到达D处,在D处测得C的仰角为75°,则建筑物的高度为( )
 如图,某人欲测量某建筑物的高度BC,在A处测得建筑物顶端C的仰角为30°,然后,向建筑物方向前进200m到达D处,在D处测得C的仰角为75°,则建筑物的高度为( )
如图,某人欲测量某建筑物的高度BC,在A处测得建筑物顶端C的仰角为30°,然后,向建筑物方向前进200m到达D处,在D处测得C的仰角为75°,则建筑物的高度为( )| A. | 50($\sqrt{3}$+1)m | B. | 50($\sqrt{2}$+1)m | C. | 50($\sqrt{3}$-1)m | D. | 50($\sqrt{3}$+$\sqrt{2}$) m |
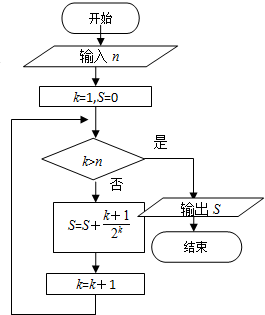
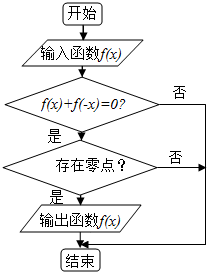 某程序框图如图所示,现输入如下四个函数,其中可以输出的函数是f(x)=sinx.
某程序框图如图所示,现输入如下四个函数,其中可以输出的函数是f(x)=sinx.