题目内容
已知各项均不相等的等差数列 的前三项和为18,
的前三项和为18,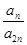 是一个与
是一个与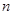 无关的常数,若
无关的常数,若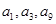 恰为等比数列
恰为等比数列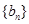 的前三项,(1)求
的前三项,(1)求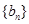 的通项公式.(2)记数列
的通项公式.(2)记数列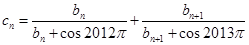 ,
,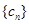 的前三
的前三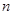 项和为
项和为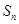 ,求证:
,求证:
(1)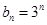 。
。
(2) 。
。
解析试题分析:(1)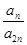 是一个与
是一个与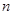 无关的常数
无关的常数 2分
2分
又

 4分
4分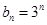 6分
6分
(2) …8分
…8分
又因为
即 ……12分
……12分
所以: ……12分
……12分
考点:等差数列、等比数列的的基础知识,数列不等式的证明,“放缩法”。
点评:中档题,本题综合考查等差数列、等比数列的基础知识,确定数列的通项公式,常常通过布列相关元素的方程组,使问题得解。数列不等式的证明问题,往往通过“放缩—求和—证明”等步骤,“错位相消法”“分组求和法”“裂项相消法”是高考常常考到数列求和方法。

练习册系列答案
相关题目
 是首项为
是首项为 ,公差为
,公差为 的等差数列
的等差数列 ,
, 是其前
是其前 项和.
项和. ,
, ,求数列
,求数列 ,
,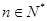 ,且
,且 、
、 、
、 成等比数列,证明:
成等比数列,证明: .
. 的前
的前 项和为
项和为 ,对任意正整数
,对任意正整数 ,记
,记 .
.  ,
, 的值;
的值; 的通项公式;
的通项公式; 求证:对任意
求证:对任意 .
. 的前
的前 项和为
项和为 ,且
,且 是
是 的等差中项,等差数列
的等差中项,等差数列 满足
满足 ,
, .
. ,数列
,数列 的前
的前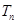 ,证明:
,证明: .
.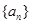 满足:
满足: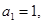 点
点 均在直线
均在直线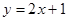 上.
上.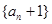 为等比数列,并求出数列
为等比数列,并求出数列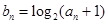 ,求数列
,求数列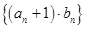 的前
的前 项和
项和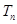 .
. 的前
的前 项和为
项和为 ,满足
,满足 且
且 构成等比数列.
构成等比数列. ;
; .
. 的前
的前 项和为
项和为 .已知
.已知 ,
, ,
, .
. 的值;
的值; .
.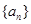 满足
满足 ,其中
,其中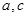 为实数,且
为实数,且 ,
, 时数列
时数列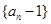 是等比数列,并求
是等比数列,并求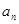 ;
;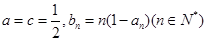 ,求数列
,求数列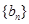 的前
的前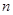 项和
项和 ;
; ,记
,记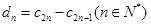 ,设数列
,设数列 的前
的前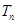 ,求证:对任意正整数
,求证:对任意正整数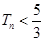 .
.