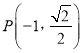题目内容
【题目】已知公差大于零的等差数列{an}的前n项和为Sn ， 且满足a3a4=117，a2+a5=22．
（1）求通项an；
（2）若数列{bn}满足bn= 
，是否存在非零实数c使得{bn}为等差数列？若存在，求出c的值；若不存在，请说明理由．
【答案】
（1）解：由等差数列的性质，得a3+a4=a2+a5=22，
又∵a3a4=117，∴a3、a4是方程x2﹣22x+117=0的解，
结合公差大于零，解得a3=9，a4=13，
∴公差d=a4﹣a3=13﹣9=4，首项a1=a3﹣2d=1．
因此，数列{an}的通项公式为an=a1+（n﹣1）d=1+4（n﹣1）=4n﹣3
（2）解：由（1）知：Sn= 
=2n2﹣n，
所以bn= 
= 
．
故b1= 
，b2= 
，b3= 
．
令2b2=b1+b3，即 
= + ，化简得2c2+c=0．
因为c≠0，故c=﹣ 
，此时bn= 
=2n．
当n≥2时，bn﹣bn﹣1=2n﹣2（n﹣1）=2，符合等差数列的定义
∴c=﹣ 时，bn=2n．（n∈N+）
由此可得，当c=﹣ 时，{bn}成以2为首项、公差为2的等差数列
【解析】（1）根据等差数列的性质，得出a3、a4是方程x2﹣22x+117=0的解，解此方程得a3=9且a4=13，再求出{an}的首项和公差，即可得到数列{an}的通项公式；（2）由（1）的结论，化简得bn= ．分别令n=1、2、3，得到{bn}的前3项，由2b2=b1+b3解出c=﹣ ，再将c=﹣ 回代加以检验，即可得到当c=﹣ 时，{bn}成以2为首项、公差为2的等差数列．
【考点精析】利用等差数列的前n项和公式和等差关系的确定对题目进行判断即可得到答案，需要熟知前n项和公式：
；如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，即
－
=d ，（n≥2，n∈N）那么这个数列就叫做等差数列．
